Maiņstrāvas kondensatori

Kas ir maiņstrāva?

Ja mēs uzskatām līdzstrāvu, tad tā ne vienmēr var būt pilnīgi nemainīga: spriegums avota izejā var būt atkarīgs no akumulatora vai galvaniskā akumulatora slodzes vai izlādes pakāpes. Pat ar nemainīgu stabilizētu spriegumu strāva ārējā ķēdē ir atkarīga no slodzes, kas apstiprina Ohma likumu. Izrādās, ka tā nav arī gluži pastāvīga strāva, taču arī šādu strāvu nevar saukt par mainīgu, jo tā nemaina virzienu.

Mainīgo lielumu parasti sauc par spriegumu vai strāvu, kura virziens un lielums nemainās ārēju faktoru, piemēram, slodzes, ietekmē, bet ir pilnīgi "neatkarīgs": šādi ģenerators to ģenerē. Turklāt šīm izmaiņām jābūt periodiskām, t.i. atkārtošanās noteiktā laika posmā, ko sauc par periodu.

Ja jebkurā gadījumā mainās spriegums vai strāva, neuztraucoties par frekvenci un citām likumsakarībām, šādu signālu sauc par troksni. Klasisks piemērs ir “sniegs” televizora ekrānā ar vāju apraides signālu. Dažu periodisku elektrisko signālu piemēri ir parādīti 1. attēlā.

Līdzstrāvai ir tikai divi raksturlielumi: avota polaritāte un spriegums. Maiņstrāvas gadījumā ar šiem diviem lielumiem acīmredzami nepietiek, tāpēc parādās vēl vairāki parametri: amplitūda, frekvence, periods, fāze, tūlītēja un efektīva vērtība.

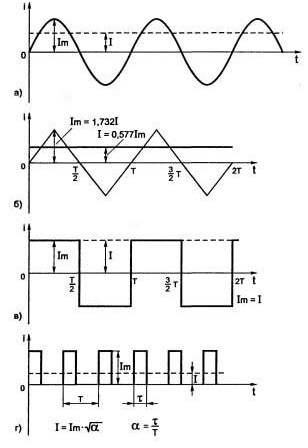
1. attēlsDažu periodisku elektrisko signālu piemēri

Tehnoloģijās visbiežāk jārisina sinusoidālās svārstības, turklāt ne tikai elektrotehnikā. Iedomājieties automašīnas riteni. Vienmērīgi braucot pa labu gludu ceļu, riteņa centrs apraksta taisnu līniju, kas ir paralēla ceļa virsmai. Tajā pašā laikā jebkurš riteņa perifērijas punkts pārvietojas pa sinusoīdu attiecībā pret tikko pieminēto līniju.

Iepriekšminēto var apstiprināt ar 2. attēlu, kurā parādīta sinusoīda konstruēšanas grafiskā metode: kurš labi studējis zīmēšanu, zina, kā veikt šādas konstrukcijas.

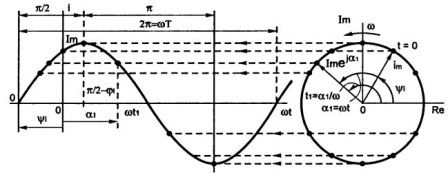
2. attēlsGrafiskā sinusoidālā viļņa metode

No fizikas skolas kursa ir zināms, ka sinusoīds ir visizplatītākais un piemērots periodiskas līknes izpētei. Tieši tādā pašā veidā sinusoidālās svārstības tiek iegūtas ģeneratorito mehāniskās ierīces dēļ.

3. attēlā parādīta sinusoidālās strāvas diagramma.

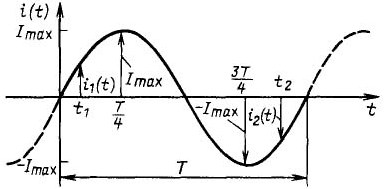
3. attēlsSinusoidālā strāva

Ir viegli redzēt, ka strāvas stiprums mainās ar laiku, tāpēc ordinātu ass ir parādīta attēlā kā i (t), ir strāvas un laika funkcija. Pilnu strāvas periodu norāda ar stabilu līniju un tam ir T. T. Ja jūs sākat apsvērumu no sākuma, jūs varat redzēt, ka sākumā strāva palielinās, sasniedz Imax, iet caur nulli, samazinās līdz –Imax, pēc tam palielinās un sasniedz nulli. Tālāk sākas nākamais laika posms, kā parādīts ar pārtraukto līniju.

Matemātiskas formulas veidā pašreizējo uzvedību uzraksta šādi: i (t) = Imax * sin (ω * t ± φ).

Šeit i (t) ir strāvas momentānā vērtība, atkarībā no laika, Imax ir amplitūdas vērtība (maksimālā novirze no līdzsvara stāvokļa), ω ir apļveida frekvence (2 * π * f), φ ir fāzes leņķis.

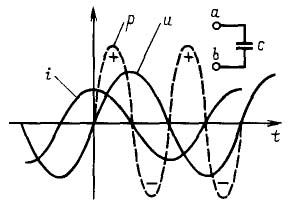
Apļveida frekvenci ω mēra radiānos sekundē, bet fāzes leņķi φ - radiānos vai grādos. Pēdējam ir jēga tikai tad, ja ir divas sinusoidālas strāvas. Piemēram, ķēdēs ar kondensators strāva ir priekšā spriegumam par 90˚ vai tieši par ceturtdaļu perioda, kā parādīts 4. attēlā. Ja ir viena sinusoidālā strāva, tad varat to pārvietot pa ordinātu asi, kā vēlaties, un no tā nekas nemainīsies.

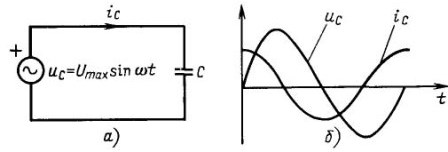
4. attēls Ķēdēs ar kondensatoru strāva pārsniedz spriegumu par ceturtdaļu perioda

Apļveida frekvences The fiziskā nozīme ir tā, kāds leņķis radiānos vienā sekundē “izies cauri” sinusoidam.

Periods - T ir laiks, kurā sinusa vilnis veiks vienu pilnīgu svārstību. Tas pats attiecas uz dažādas formas vibrācijām, piemēram, taisnstūrveida vai trīsstūrveida. Periodu mēra sekundēs vai mazākās vienībās: milisekundēs, mikrosekundēs vai nanosekundēs.

Cits jebkura periodiska signāla, ieskaitot sinusoīdu, parametrs ir frekvence, cik daudz svārstību signāls veiks 1 sekundē. Frekvences mērvienība ir Hercs (Hz), kas nosaukts 19. gadsimta zinātniekam Heinriham Hercam. Tātad, frekvence 1 Hz ir nekas vairāk kā viena svārstība sekundē. Piemēram, apgaismojuma tīkla frekvence ir 50Hz, tas ir, precīzi 50 sinusoidālie periodi pāriet sekundē.

Ja pašreizējais periods ir zināms (varat mēra ar osciloskopu), tad signāla frekvence palīdzēs noskaidrot formulu: f = 1 / T. Turklāt, ja laiks tiek izteikts sekundēs, rezultāts būs hercos. Un otrādi, T = 1 / f, frekvence Hz, laiku iegūst sekundēs. Piemēram, kad 50 herci periods būs 1/50 = 0,02 sekundes vai 20 milisekundes. Elektroenerģijā biežāk tiek izmantotas augstākas frekvences: KHz - kiloherci, MHz - megaherci (tūkstošiem un miljoniem svārstību sekundē) utt.

Viss, kas teikts par strāvu, attiecas arī uz maiņstrāvu: 6. attēlā ir pietiekami vienkārši mainīt burtu I uz U. Formula izskatīsies šādi: u (t) = Umax * sin (ω * t ± φ).

Šie skaidrojumi ir pietiekami, lai atgrieztos pie eksperimentēt ar kondensatoriem un izskaidrot viņu fizisko nozīmi.

Kondensators vada maiņstrāvu, kas parādīta diagrammā 3. attēlā (skat. Rakstu - Kondensatori maiņstrāvas elektroietaisēm) Lampas spilgtums palielinās, kad ir pievienots papildu kondensators. Kad kondensatori ir savienoti paralēli, to kapacitātes vienkārši saskaitās, tāpēc var pieņemt, ka kapacitāte Xc ir atkarīga no kapacitātes. Turklāt tas ir atkarīgs arī no strāvas frekvences, un tāpēc formula izskatās šādi: Xc = 1/2 * π * f * C.

No formulas izriet, ka palielinoties mainīga sprieguma kapacitātei un frekvencei, reaģētspēja Xc samazinās. Šīs atkarības ir parādītas 5. attēlā.

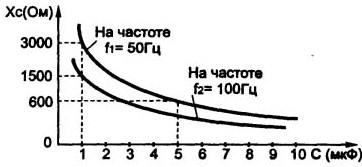
5. attēls. Kondensatora reaģētspējas atkarība no kapacitātes

Ja formulā aizstāsim frekvenci hercos, bet kapacitāti Farados, tad rezultāts būs Ohms.

Vai kondensators sakarsīs?

Tagad atcerieties pieredzi ar kondensatoru un elektrisko skaitītāju, kāpēc tas neizgriežas? Fakts ir tāds, ka skaitītājs ņem vērā aktīvo enerģiju, ja patērētājs ir tīri aktīva slodze, piemēram, kvēlspuldzes, elektriskā tējkanna vai elektriskā plīts. Šādiem patērētājiem spriegums un strāva sakrīt fāzē, ir viena zīme: ja reizināt divus negatīvos skaitļus (spriegumu un strāvu negatīvā puscikla laikā), rezultāts saskaņā ar matemātikas likumiem joprojām ir pozitīvs. Tāpēc šādu patērētāju iespējas vienmēr ir pozitīvas, t.i. nonāk slodzē un izdalās siltuma veidā, kā parādīts 6. attēlā ar pārtraukto līniju.

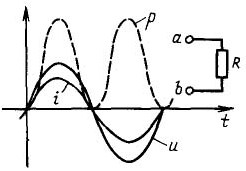
6. attēls

Gadījumā, ja kondensators ir iekļauts maiņstrāvas ķēdē, strāva un spriegums nesakrīt fāzē: strāva ir 90 оп pirms fāzes sprieguma, kas noved pie kombinācijas, kad strāvai un spriegumam ir atšķirīgas pazīmes.

7. attēls

Šajos brīžos vara ir negatīva. Citiem vārdiem sakot, ja jauda ir pozitīva, kondensators tiek uzlādēts, un, ja tas ir negatīvs, uzkrātā enerģija tiek nodota atpakaļ avotā. Tāpēc vidēji tas izrādās pa nullēm un šeit vienkārši nav ko ieskaitīt.

Kondensators, pat ja tas, protams, nav izmantojams, nemaz nesasilst. Tāpēc bieži kondensators, ko sauc par brīvo pretestību, kas to ļauj izmantot mazjaudas barošanas avotos bez transformatoriem.Kaut arī šādi bloki nav ieteicami to bīstamības dēļ, tomēr dažreiz tas ir jādara.

Pirms uzstādīšanas šādā ierīcē rūdīšanas kondensators, tas jāpārbauda ar vienkāršu savienojumu ar tīklu: ja pusstundas laikā kondensators nav uzkarsējis, tad to var droši iekļaut ķēdē. Pretējā gadījumā jums tas vienkārši jāizmet, nenožēlojot.

Ko rāda voltmetrs?

Ražojot un remontējot dažādas ierīces, lai arī tas nav ļoti bieži, ir jāmēra maiņstrāvas un pat strāvas. Ja sinusoīds uzvedas tik drudžaini, tad uz augšu un uz leju, ko parādīs parasts voltmetrs?

Periodiskā signāla, šajā gadījumā sinusoīda, vidējo vērtību aprēķina kā laukumu, ko ierobežo abscisas ass, un signāla grafisko attēlu, kas dalīts ar 2 * π radiāniem, vai sinusoīda periodu. Tā kā augšējā un apakšējā daļa ir absolūti identiskas, bet tām ir atšķirīgas pazīmes, sinusoīda vidējā vērtība ir nulle, un tas vispār nav jāmēra, un tas ir pat vienkārši bezjēdzīgs.

Tāpēc mērīšanas ierīce parāda mums sprieguma vai strāvas vidējo vērtību. Vidējā kvadrāta vērtība ir tāda periodiskās strāvas vērtība, pie kuras uz to pašu slodzi izdalās tāds pats siltuma daudzums kā līdzstrāvai. Citiem vārdiem sakot, spuldze spīd ar tādu pašu spilgtumu.

To raksturo šādas formulas: Icrc = 0,707 * Imax = Imax / √2 spriegumam, formula ir vienāda, vienkārši nomainiet vienu burtu Ucrc = 0,707 * Umax = Umax / √2. Tieši šīs vērtības parāda mērīšanas ierīce. Tos var aizstāt formulās, veicot aprēķinus saskaņā ar Ohma likumu vai aprēķinot jaudu.

Bet tas nav viss, uz ko spēj kondensators maiņstrāvas tīklā. Nākamajā rakstā mēs apsvērsim kondensatoru izmantošanu impulsa ķēdēs, augstas caurlaides un zemas caurlaides filtros, sinusoidālo un kvadrātveida viļņu ģeneratoros.

Boriss Aladyshkin

Raksta turpinājums: Kondensatori elektroniskās shēmās