Kondensatori elektroniskās shēmās

Iepriekšējos rakstos mēs īsumā runājām par kondensatoru darbību maiņstrāvas ķēdēs, kā un kāpēc kondensatori iziet maiņstrāvu (sk. Maiņstrāvas kondensatori) Šajā gadījumā kondensatori nesasilda, viņiem netiek piešķirta jauda: vienā sinusoīda pusviļņā kondensators uzlādējas, bet otrā tas dabiski izlādējas, vienlaikus nododot uzkrāto enerģiju atpakaļ strāvas avotā.

Šī strāvas caurlaides metode ļauj izsaukt kondensatoru par brīvu pretestību, un tieši tāpēc kontaktors, kas savienots ar kontaktligzdu, neveic skaitītāja griešanos. Un tas viss tāpēc, ka strāva kondensatorā pārsniedz tieši 1/4 no laika, kad tam tiek piemērots spriegums.

Bet šī fāzes virzība ļauj ne tikai “pievilināt” skaitītāju, bet arī ļauj izveidot dažādas shēmas, piemēram, sinusoidālu un taisnstūrveida signālu ģeneratorus, laika kavējumus un dažādus frekvences filtrus.

Šī stāsta procesā dažreiz būs jāatgādina jau iepriekš teiktais, tā sakot, apkopot. Tas palīdzēs neatgriezties pie iepriekšējiem rakstiem, lai atgādinātu vienkāršu formulu vai vienkārši “kas tas ir?”

Kondensatoru paralēlais un virknes savienojums

Ar paralēlu kondensatoru savienojumu kopējā jauda ir vienkārši jaudu aritmētiskā summa. Protams, ar šo iekļaušanu kopējā kapacitāte būs lielāka nekā lielākā kondensatora kapacitāte. Ctotal = C1 + C2 + C3 + ... + Cn.

Sērijveida savienojuma gadījumā kopējā jauda ir mazāka nekā mazākā.

1 / Ctotal = 1 / C1 + 1 / C2 + 1 / C3 + ... + 1 / Cn.

Kad divi identiski kondensatori ir savienoti virknē, kopējā kapacitāte būs vienāda ar pusi no vienas kapacitātes: piemēram, savienojot divus kondensatorus pa 1 μF katram, kopējā kapacitāte būs 0,5 μF.

Kapacitāte Xc

Šeit viss, tāpat kā savienojot rezistorus, ir tikai pilnīgi pretējs: virknes savienojums samazina kopējo kapacitāti, bet paralēlais - to palielina. Pieslēdzot kondensatorus, šo apstākli nevajadzētu aizmirst, jo kapacitātes palielināšanās samazina kapacitātes Xc samazināšanos

Xc = 1/2 * π * f * C.

No matemātikas viedokļa tas ir diezgan dabiski, jo ietilpība C ir frakcijas saucējā. Starp citu, frekvence f atrodas tajā pašā vietā, tāpēc frekvences palielināšanās noved arī pie kapacitātes Xc samazināšanās. Fiziskā nozīme ir tāda, ka caur to pašu kondensatoru ir labāk, netraucētāk, ka augstas frekvences iziet cauri. Tas tiks apspriests nedaudz vēlāk, kad runa ir par zemas caurlaides un augstas caurlaides filtriem.

Ja mēs ņemam kondensatoru ar ietilpību 1 μF, tad frekvencei 60 Hz tā Xc būs 2653 omi, bet frekvencei 400 Hz tam pašam kondensatoram ir Xc tikai 398 omi. Tie, kas vēlas, var pārbaudīt šos rezultātus pēc formulas, aizstājot π = 3,14, frekvenci hercos un kapacitāti fāzēs. Tad rezultāts būs omi. Visam jāatbilst SI sistēmai!

Bet kondensatori tiek izmantoti ne tikai kā brīvu slāpējošu slāpēšanas pretestību vai taisngrieža filtros. Bez viņu līdzdalības zemu un augstas frekvences ģeneratoru shēmas, dažādi viļņu formas pārveidotāji, diferencējošas un integrējošas shēmas, pastiprinātāji un citas shēmas.

Tālāk tiks apskatīti dažādi elektriskie signāli, ar kuriem kondensatoriem jāstrādā. Pirmkārt, šie ir periodiski signāli, kas piemēroti novērošanai ar osciloskops.

Svārstību periods un biežums

Tāpēc periodiskas svārstības sauc par periodiskām, kas, neapstājoties, atkārto to pašu formu, piemēram, vienu sinusoidālu svārstību. Šīs pilnās šūpoles ilgumu precīzi sauc par periodu T, un to mēra sekundēs, milisekundēs un mikrosekundēs.Mūsdienu elektronika nodarbojas pat ar nanosekundēm (sekundes miljardo daļu).

Periodu skaitu sekundē sauc par svārstību frekvenci (cik bieži) f un izsaka hercos. 1Hz ir frekvence, kurā vienas svārstības ar vienu pilnu periodu tiek veiktas 1 sekundē. Perioda un biežuma attiecību izsaka ar vienkāršu formulu T = 1 / f.

Attiecīgi, zinot svārstību periodu, ir ļoti vienkārši aprēķināt frekvenci f = 1 / T.

Tādā veidā tiek aprēķināta frekvence, veicot mērījumus ar osciloskopu: tiek aprēķināts šūnu skaits periodā, kas reizināts ar vienas šūnas ilgumu, un periodu iegūst, piemēram, mikrosekundēs. Un, lai uzzinātu frekvenci, viņi vienkārši izmantoja pēdējo formulu.

Parasts elektroniskais osciloskops Ļauj novērot tikai periodiskus signālus, kurus var sinhronizēt ar svārstību frekvenci, lai iegūtu izpētei piemērotu nekustīgu attēlu. Ja nosūtāt signālu mūzikas programmai uz osciloskopa ievadi, jūs neko nevarēsit apturēt. Lai novērotu šādus signālus, tiek izmantoti glabāšanas osciloskopi.

Ja periodu mēra milisekundēs, frekvenci iegūst kilohercos, par periodu, ko mēra ar mikrosekundēm, frekvence jau tiek izteikta megahercos. Tas ir, ja jūs neievēroat SI sistēmas prasības: periods sekundēs, frekvence hercos.

Nesinzoidālas vibrācijas

Kā minēts iepriekš, sinusa vilnis ir visizplatītākais un piemērotākais periodiskās līknes izpētei un praktiskai izmantošanai. Rūpnieciskos apstākļos to iegūst, izmantojot elektriskos ģeneratorus, piemēram, hidroelektrostacijās. Elektroniskajās ierīcēs tiek izmantotas visdažādāko formu vibrācijas.

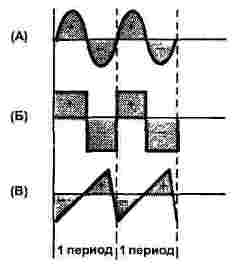
Pamatā tās ir trīs formas: sinusoidāla, taisnstūrveida un trīsstūrveida, kā parādīts 1. attēlā. Gan strāvai, gan spriegumam var būt šāda forma, tāpēc attēlā ir parādīta tikai laika ass, ordinātu ass ir atstāta bez nosaukuma.

Šādas svārstības rada īpašas elektroniskas shēmas. Taisnstūra un trīsstūra signālus bieži sauc par impulsa. Tomēr ir ļoti daudz elektronisko shēmu, kas veic signāla pārveidi: piemēram, no sinusoīda var izgatavot taisnstūri vai trīsstūri.

1. attēls

Visiem trim signāliem attēls parāda divus periodus, visiem signāliem ir vienāda frekvence.

Nesinusoidālo signālu spektrs

Jebkuru elektrisko signālu var attēlot kā amplitūdas mērījumu kādā brīdī. Šo paraugu frekvenci sauc par paraugu ņemšanas frekvenci, un tā ir vismaz divas reizes augstāka par izmērītā signāla augšējo frekvenci. Pēc tam no šiem paraugiem jūs varat atjaunot sākotnējo signālu. Šo metodi izmanto, piemēram, digitālā skaņas ierakstīšanā. Šo metodi sauc arī par laika analīzi.

Cita metode paredz, ka jebkuru signālu, pat taisnstūrveida, var attēlot kā sinusoīdu algebrisko summu ar dažādām frekvencēm un fāzēm. Šo metodi sauc par frekvences analīzi. Bet tas, kas tika teikts “ar dažādām frekvencēm”, nav pilnīgi taisnība: sinusoīdus veidojošos elementus sauc par harmonikām, un to frekvences ievēro noteiktus likumus.

Sinusoidālo vilni, kura frekvence ir vienāda ar kvadrātveida viļņa frekvenci, sauc par pamata harmoniku. Pāra harmonikas iegūst, reizinot pamata frekvenci ar pāra skaitli, un nepāra harmonikas - attiecīgi ar nepāra.

Tādējādi, ja pirmās harmonikas frekvence ir 1000 Hz, tad otrā ir 2000 Hz, ceturtā ir 4000 Hz utt. Nepāra harmonikām būs frekvences 3000Hz, 5000Hz. Turklāt katra harmonika ir mazāka amplitūdā nekā galvenā: jo augstāka harmonika, jo mazāka amplitūda.

Mūzikā harmonikas sauc par virsotnēm. Tieši viņi veido skaņas tembru, ļauj atšķirt vijoli no klavierēm, bet ģitāru - no saksofona. Tie neļauj sajaukt vīrieša un sievietes balsi vai atšķirt Petrovu no Ivanova. Un tikai pats sinusoīds vairs nevar tikt sadalīts vai salikts no jebkādiem signāliem.

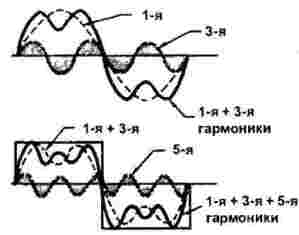
2. attēlā parādīta taisnstūra impulsa uzbūve.

2. attēls

Pirmā un trešā harmonika ir parādīta attēla augšējā daļā. Ir viegli redzēt, ka viena pirmā harmoniskā perioda laikā trīs trešās pārejas periodi. Šajā gadījumā trešās harmonikas amplitūda ir viena trešdaļa no pirmās. Šeit parādīta arī pirmās un trešās harmonikas summa.

Zemāk kopā ar 1 un 3 harmoniku parādītas vēl 5 harmonikas: taisnstūra signāla periodam tas izdodas veikt tieši piecus periodus. Šajā gadījumā tā amplitūda ir vēl mazāka, precīzāk, precīzi 1/5 no galvenā (pirmā). Bet nevajadzētu domāt, ka viss beidzas ar piekto harmoniku: to vienkārši nevar parādīt attēlā, patiesībā ir daudz vairāk.

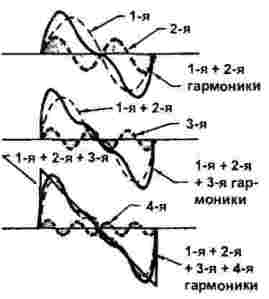
Zāģa un trīsstūrveida signālu veidošanās, kas parādīta 3. attēlā, ir nedaudz sarežģītāka.Ja iepriekšējā gadījumā piedalījās tikai nepāra harmonikas, tad spēlē pat harmonikas.

3. attēls

Tādējādi mēs varam apgalvot, ka ar daudzu harmoniku palīdzību tiek sintezēts jebkuras formas signāls, un harmoniku skaits un tips ir atkarīgs no viļņu formas, kā parādīts 2. un 3. attēlā.

Remontējot un uzstādot elektronisko aprīkojumu, elektrisko signālu izpētei tiek izmantots osciloskops. Tas ļauj apsvērt periodisko signālu formu, to amplitūdu, izmērīt atkārtojuma periodu. Bet 2. un 3. attēlā parādītās harmonikas nevar redzēt.

Pat ja jūs, piemēram, ar osciloskopu savienojat elektrisko ģitāru, velciet vienu stīgu, ekrānā parādās sinusoīds, tā ir arī pirmā harmonika. Šajā gadījumā nevar būt runas par jebkādiem virsskaņiem. Tas pats sinusoīds radīsies, ja iepūsīsit caurulē vai flautu mikrofona priekšā.

Kā iegūt taisnstūrveida impulsus

Pēc iepazīšanās ar elektriskajiem signāliem mums jāatgādina kondensatori, ar kuriem raksts sākās. Pirmkārt, jums vajadzētu iepazīties ar vienu no klasiskās elektronikas shēmām - multivibrators, (4. attēls) taisnstūrveida impulsus ģenerē tieši viņš. Ķēde ir tik klasiska, ka tā sāk darboties uzreiz, neprasot nekādus iestatījumus vai pielāgojumus.

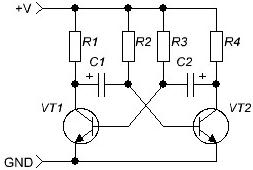
4. attēls

Multivibrators ir divpakāpju pastiprinātājs, par kuru saņem pozitīvas atsauksmes. Ja kolektora slodzes rezistori R1 = R4, bāzes rezistori R2 = R3 ir vienādi, un kondensatori C1 = C2 ir vienādi, multivibratoru sauc par simetrisku un ģenerē meander tipa kvadrātveida viļņu impulsus - impulsa ilgums ir vienāds ar pauzes ilgumu.

Šādu impulsu darba cikls (perioda un impulsa ilguma attiecība) ir vienāds ar diviem. Angļu valodas shēmās viss ir tieši pretējs: viņi to sauc par darba ciklu. To aprēķina kā impulsa ilguma attiecību pret tā pēctecības periodu un izsaka procentos. Tādējādi līkumainiecei darba cikls ir 50%.

Vai dators ir pareizs?

Nosaukumu multivibrators ierosināja holandiešu fiziķis van der Pols, jo taisnstūra signāla spektrā ir daudz harmoniku. To var pārbaudīt, ja radioviļņu uztvērēju, kas darbojas vidēja viļņa diapazonā, varat novietot netālu no multivibratora, kas darbojas pat ar audio frekvenci: no skaļruņa skanēs gavilēšana. Tas liek domāt, ka multivibrators papildus skaņas frekvencei izstaro arī augstas frekvences svārstības.

Ražošanas frekvences noteikšanai var izmantot formulu f = 700 / (C1 * R2).

Izmantojot šo formulas formu, kondensatora kapacitāte mikrofaradās (μF), pretestība kilo-omi (KΩ), rezultāts ir hercos (Hz). Tādējādi frekvenci nosaka ar ķēdes C1 * R2 laika konstanti; kolektora slodzes frekvenci neietekmē. Ja mēs ņemam C1 = 0,02 μF, R2 = 39 KΩ, tad iegūstam f = 700 / (0,02 * 39) = 897,4 Hz.

Multivibrators datoru un mikrokontrolleri Saskaņā ar šo shēmu to gandrīz nekad neizmanto, lai gan tas var būt piemērots dažādiem eksperimentiem. Pirmkārt, izmantojot datorus. Šādi izskatās multivibratoru shēma, kas samontēta programmā Multisim. Šeit parādīts arī osciloskopa savienojums.

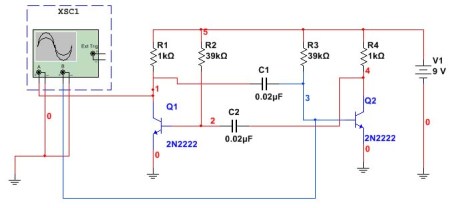
5. attēls

Šajā shēmā kondensatori un rezistori ir uzstādīti tāpat kā iepriekšējā piemērā. Uzdevums ir pārbaudīt aprēķinu pēc formulas, vai tiks iegūta tāda pati frekvence. Lai to izdarītu, izmēriet impulsu periodu un pēc tam pārrēķiniet tos frekvencē. Multisim osciloskopa rezultāts ir parādīts 6. attēlā.

6. attēls

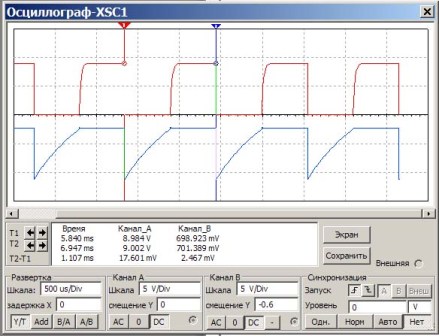
Daži skaidrojumi 6. attēlam.

Osciloskopa ekrānā sarkans impulss parāda impulsus uz tranzistora kolektora, bet zils - uz pamatiem. Zem ekrāna lielā baltā logā skaitļi parāda mērījumu rezultātus. Mēs esam ieinteresēti kolonnā "Laiks". Laiku mēra ar indikatoriem T1 un T2 (sarkani un zili trīsstūri virs ekrāna).

Tādējādi impulsu atkārtošanās periods T2-T1 = 1,107ms ir parādīts diezgan precīzi. Atliek tikai aprēķināt frekvenci f = 1 / T = 1 / 1,107 * 1000 = 903Hz.

Rezultāts ir gandrīz tāds pats kā aprēķinā saskaņā ar formulu, kas tiek dota nedaudz augstāka.

Kondensatorus var izmantot ne tikai atsevišķi: apvienojumā ar rezistoriem tie ļauj vienkārši izveidot dažādus filtrus vai izveidot fāzes nobīdes shēmas. Bet tas tiks apspriests nākamajā rakstā.

Raksta turpinājums: Kondensatori elektroniskās shēmās. 2. daļa

Boriss Aladyshkin