Algebra boolowska. Część 2. Podstawowe prawa i funkcje

Kontynuacja opowieści o algebrze boolowskiej, konwencjach, regułach, operacjach. Przejście do podstaw obwodów stykowych.

W pierwszy artykuł George Bull został opisany jako twórca algebry logiki. W drugim artykule opisano podstawowe operacje algebry boolowskiej oraz metody upraszczania wyrażeń boolowskich. Tak więc algebra boolowska używa oświadczeń jako argumentów, a nie ich znaczenia, ale prawdziwości lub fałszu oświadczenia.

Formularz do pisania wyrażeń w algebrze logicznej.

Jeśli stwierdzenie jest prawdziwe, wówczas jest napisane w następujący sposób: A = 1, jeśli jest fałszywe, to A = 0 (w końcu nieprawdą jest, że ziemniak jest owocem). W przypadku każdej instrukcji A ma wartość true (A = 1) lub false (A = 0). Tu nie może być środka. Już o tym rozmawialiśmy.

Jeśli połączysz dwie proste instrukcje ze związkiem, otrzymasz złożoną instrukcję, która nazywa się produktem logicznym. Weźmy dwa proste powiedzenia: „Trzy to więcej niż dwa” oznaczymy literą A, „Trzy mniej niż pięć” - literą B.

Stąd złożone stwierdzenie „Trzy to więcej niż dwa, a mniej niż pięć” jest logiczne (w tym przypadku wielka litera I mówi, że jest to operacja logiczna „ORAZ”, a także później w tekście „LUB” i „NIE”). i B. Jest oznaczony w następujący sposób: A ^ B lub A * B.

Mnożenie logiczne (operacja „AND”).

W algebrze elementarnej A * A = A2. Ale w algebrze Buhla A * A = A2 = A, A * A = A, ponieważ znak mnożenia (*) oznacza teraz ... I ... w znaczeniu And ... I. Całe nasze doświadczenie potwierdza, że ​​A&A jest taki sam jak sam A. Nie można się z tym nie zgodzić. Prawdziwość tego stwierdzenia nie zmienia się, jeśli zostanie kilkakrotnie powtórzone.

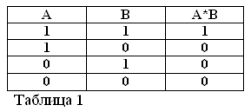
Iloczyn dwóch stwierdzeń jest uważany za prawdziwy (równy 1) i tylko wtedy, gdy oba czynniki są prawdziwe, i fałszywy (równy 0), jeśli co najmniej jeden z czynników jest fałszywy. Zgadzam się, że reguły te nie są sprzeczne ze zdrowym rozsądkiem, a ponadto są w pełni zgodne z zasadami algebry elementarnej:

1*1 = 1, 1*0 = 0 = 0*1 = 0, 0*0 = 0.

Pierwsza równość brzmi następująco: jeśli zarówno A, jak i B są prawdziwe, to iloczyn A * B jest prawdziwy. W algebrze Buhl znak mnożenia (*) zastępuje związek I.

Produkty logiczne mogą zawierać nie dwa, ale większą liczbę stwierdzeń - czynników. I w tym przypadku produkt jest prawdziwy tylko wtedy, gdy jednocześnie wszystkie stwierdzenia-czynniki są prawdziwe.

Dodawanie logiczne (operacja LUB)

Jeśli dwie instrukcje są połączone przez związek LUB. utworzone zdanie złożone nazywa się sumą logiczną.

Rozważ przykład logicznej sumy. Mówiąc: „Dzisiaj pójdę do kina”.

Oświadczenie B: „Dzisiaj pójdę na dyskotekę”. Dodajemy oba stwierdzenia i otrzymujemy: „Dzisiaj pójdę do kina LUB na dyskotekę”.

Ta złożona instrukcja jest oznaczona następująco: A + B = C lub (A V B) = C.

Przez C oznaczono złożoną instrukcję sumy logicznej.

W omawianym przykładzie nie można używać związku OR w wyłącznym znaczeniu. Rzeczywiście tego samego dnia można dostać się do kina i na dyskotekę. A oto powiedzenie:

„Przewodniczącym partnerstwa ogrodniczego będzie Pietrow lub Iwanow”, to nie jest logiczna suma, ponieważ tylko jedna osoba będzie przewodniczącym, a druga będzie zwykłym ogrodnikiem-amatorem.

Wybrano znak V sumy logicznej, ponieważ jest to pierwsza litera łacińskiego słowa „vel”, co oznacza „lub”, w przeciwieństwie do łacińskiego słowa „aut>”, co oznacza „i”. Teraz powinno być jasne dla wszystkich, dlaczego logiczny produkt jest oznaczony znakiem ^.

W algebrze elementarnej obowiązuje reguła A + A = 2A. Ta reguła jest prawdziwa, bez względu na to, jaką liczbę reprezentuje litera A. W algebrze boolowskiej reguła A + A = A. Odpowiada jej. Całe nasze doświadczenie życiowe mówi, że powiedzenie A LUB A lub obu A to tylko kolejny i dłuższy sposób na powiedzenie tylko A.

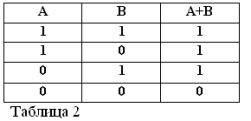
Jak każda instrukcja złożona, suma dwóch instrukcji A i B może być prawdziwa lub fałszywa. Suma jest uważana za prawdziwą, to znaczy równą jedności, jeśli co najmniej jeden z warunków jest prawdziwy:

A + B = 1, jeśli OR A = 1 OR B = 1, co jest zgodne z konwencjonalną arytmetyką:

1+0 = 0+1 = 1.

Jeśli oba zsumowane stwierdzenia są prawdziwe, wówczas suma jest również uważana za prawdziwą, dlatego w algebrze boolowskiej mamy: (1) + (1) = 1.

Nawiasy klamrowe ustawia się tutaj, aby podkreślić warunek, znaczenie tego dodatku, a nie arytmetykę.

Suma dwóch instrukcji jest uważana za fałszywą i równa zero, jeśli, ale tylko jeśli oba warunki są fałszywe. Stąd:

0 + 0=0.

Tak więc suma dwóch instrukcji A + B jest uważana za prawdę, jeśli prawda, LUB A, OR B, LUB oba warunki razem. Zatem słowo OR jest oznaczone znakiem +.

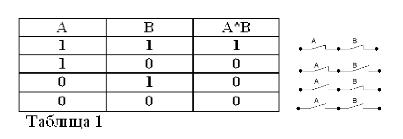
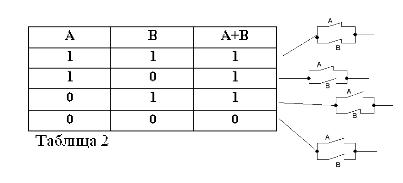
Pamiętając, że stwierdzenia A i B mogą być prawdziwe lub fałszywe, a zatem mieć miarę prawdy 1 lub 0, wyniki rozważanych operacji AND i OR można podsumować w tabelach 1 i 2.

Trzecią operacją, szeroko stosowaną przez algebrę Buhla, jest operacja negacji - NIE. Przypominamy, że algebra elementarna używa operacji DODAJ, D Odejmij, Pomnóż przez, Podziel przez i kilka innych.

Do każdego zdania A jest jego negacja NIE A, którą oznaczymy symbolem / A. To nie powinno być wątpliwości.

Podajemy przykłady: „Pójdziemy do lasu” A, „Nie pójdziemy do lasu” / A.

Jeśli twierdzenie A jest prawdziwe, to znaczy A = 1, to jego negacja / A musi być fałszywa / A = 0. I odwrotnie, jeśli dowolne zdanie jest fałszywe, to jego negacja jest prawdziwa. Na przykład: „Koń nie je siana” / A = 0, „Koń nie je siana” (A = 1). Można to wyrazić w tabeli 3.

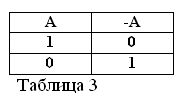
Określając znaczenie działania negacji i zakładając, że z dwóch zdań A i / A jest zawsze jedna prawda, następują dwie nowe formuły algebry boolowskiej:

A + (/ A) = 1 i A * (/ A) = 0.

Istnieją również inne formuły, które upraszczają logiczne przetwarzanie instrukcji. Na przykład 1 + A = 1, ponieważ zgodnie z definicją dodawania, w przypadku gdy jeden warunek jest równy jedności, suma jest zawsze równa jedności. Uzyskany wynik nie zależy od tego, czy A = 0 czy A = 1.

Każda z trzech analizowanych operacji logicznych (AND, OR, NOT) ma pewne właściwości zbliżone do reguł algebry elementarnej. Jeśli wszystkie zostaną sformułowane, otrzymamy 25 reguł algebry boolowskiej. Są wystarczające, aby rozwiązać prawie każdy logiczny problem. Bez tych reguł rozwiązanie problemów logicznych staje się dość trudne z powodu ich pozornej złożoności. Próba znalezienia właściwej odpowiedzi bez korzystania z reguł oznacza zastąpienie ich pomysłowością i ogólnym rozumowaniem. Reguły znacznie ułatwiają tę pracę i oszczędzają czas.

W ramach artykułu nie można rozważyć wszystkich tych 25 zasad, ale ci, którzy chcą, zawsze mogą je znaleźć w odpowiedniej literaturze.

Jak już wspomniano w pierwszym artykule z 1938 r., Młody amerykański naukowiec Claude Shannon w swoim artykule „Symboliczna analiza układów przekaźnikowych i przełączających” po raz pierwszy używa algebry Boolean do problemów technologii przekaźnikowej. Odkrycie Shannona polegało na tym, że zdał sobie sprawę, że metoda projektowania przekaźników i komputerów elektronicznych jest właściwie gałęzią logiki matematycznej.

Często się zdarza. Od wielu lat naukowiec pracuje nad problemem, który wydaje się zupełnie niepotrzebny dla jego rodaków - po prostu zabawą. Ale minęły dziesięciolecia, a czasem wieki, a teoria, której nikt nie potrzebuje, nie tylko nabywa prawo do istnienia, ale bez niego dalszy postęp staje się nie do pomyślenia.

Co pomogło Shannon po raz drugi „odkryć” algebrę boolowską? Sprawa? Nic w tym rodzaju.

Miłość do przekaźników, zbudowanych na konwencjonalnych przełącznikach i przekaźnikach, pomogła młodemu naukowcowi połączyć zapomnianą teorię z zadaniami automatycznych central telefonicznych, nad którymi wówczas pracował. Później Shannon wprowadził tę samą ideę „tak lub nie” do dyskretnych wiadomości i położył podwaliny pod całą sekcję cybernetyki - teorię informacji.

Algebra Buhla była bardzo odpowiednia do analizy i syntezy obwodów przekaźnikowych. Wystarczyło przyjąć jako prawdziwe stwierdzenie: „W obwodzie jest sygnał”, a jako fałszywe - „W obwodzie nie ma sygnału”, gdy pojawiła się nowa algebra - algebra sygnału, algebra obwodu przekaźnika.

Nowa algebra jest ważna tylko w odniesieniu do obwodów przekaźnikowych i przełączających. W końcu tylko w takich schematach spełniony jest warunek „jest sygnał” i „brak sygnału”. Gdy sygnał zmienia się w sposób ciągły, uzyskując dowolnie dużą liczbę warunków pośrednich (taki sygnał nazywa się analogowy), algebra przekaźnika nie ma zastosowania. Zawsze należy o tym pamiętać. Ale tylko większość komputerów elektronicznych i maszyn cybernetycznych stosuje dyskretną zasadę przetwarzania sygnałów, która opiera się na elementach „tak - nie”.

Wyrażenie „Kontakt zamknięty” zostało zaakceptowane przez Shannon jako prawda (1), a „Kontakt otwarty” jako fałsz (0). Reszta „algebry”, łącznie z operacjami AND, OR i NOT oraz 25 regułami, Shannon pożyczył od Boole'a.

Algebra obwodu przekaźnikowego okazała się prostsza niż algebra boolowska, ponieważ dotyczy tylko elementów typu „tak - nie”. Ponadto nowa algebra jest bardziej wizualna.

Elementami tej algebry są kontakty, które oznaczymy literami A, B, C ... Kontakt jest zamknięty - A, kontakt jest otwarty - / A (litera z myślnikiem).

Notacja, jak widać, jest całkowicie zaczerpnięta z algebry boolowskiej. Otwarty kontakt jest negacją kontaktu zamkniętego. Ten sam kontakt nie może być zarówno zamknięty, jak i otwarty.

Zgadzamy się, że jeśli w jakimkolwiek obwodzie dwa kontakty są oznaczone tą samą literą, oznacza to, że zawsze przyjmują te same wartości.

W dowolnym momencie oba są otwarte jednocześnie lub oba są zamknięte. Najłatwiejszym sposobem na wyobrażenie sobie, że są ze sobą połączone mechanicznie, aby oba z nich jednocześnie otwierały się lub zamykały.

Jeśli w jakimś łańcuchu kontakt jest zaprzeczeniem innego kontaktu, wówczas ich znaczenie jest zawsze przeciwne. Na przykład styki C i / C nigdy nie mogą być jednocześnie otwarte lub jednocześnie zamknięte. I na schemacie można je przedstawić mechanicznie połączonymi: jeśli jeden z nich otworzy się, a drugi zamknie się.

Znajomość algebry przekaźników rozpoczynamy od analizy najprostszych obwodów odpowiadających operacjom AND, OR i NOT.

Iloczyn dwóch styków (działanie AND) to obwód uzyskany w wyniku ich szeregowego połączenia: jest zamknięty (równy 1) tylko wtedy, gdy oba styki są zamknięte (równy 1).

Suma dwóch styków (operacja OR) będzie obwodem utworzonym, gdy zostaną połączone równolegle: jest zamknięty (równy 1), gdy co najmniej jeden ze styków tworzących obwód jest zamknięty (równy 1).

Przeciwieństwem tego styku (operacja NIE) jest styk równy 0 (otwarty), jeśli styk ten ma wartość 1 (zamknięty) i odwrotnie.

Podobnie jak w algebrze boolowskiej, jeśli kontakty oznaczone są literami A i B, to iloczyn dwóch kontaktów oznaczymy A * B, suma A + B, a kontakt przeciwny A, przez / A. Powyższe wyjaśniono na rycinach 1, 2 i 3.

Ważność tabel odpowiadających operacjom AND, OR i NOT. teraz nikt nie powinien mieć wątpliwości.

Zastanówmy się nad dwoma przykładami: 1 * 0 = 0 i 1 + 0 = 1.

Z rysunku wynika, że ​​styk trwale zamknięty połączony szeregowo ze stykiem trwale otwartym jest równoważny stykowi trwale otwartemu (1 * 0 = 0) Styk zamknięty trwale połączony równolegle ze stykiem stale otwartym jest równoważny stykowi trwale zamkniętemu.

Po zapoznaniu się z arytmetyką obwodów stykowych można opisać dowolny obwód przekaźnika za pomocą wzoru przy użyciu przyjętych konwencji. W cybernetyki takie formuły nazywane są strukturalne.

Jeśli wzór strukturalny dowolnego obwodu przekaźnika wynosi 1, wówczas sygnał może przez niego przejść - obwód jest zamknięty. I odwrotnie, jeśli wzór strukturalny obwodu wynosi 0, sygnał nie przejdzie przez niego - obwód zostanie przerwany.Wniosek: dwa obwody przekaźnikowe są sobie równe, gdy ich wzory strukturalne są równe.

W dalszej części artykułu rozważymy przykłady obwodów stykowych, typowych obwodów stykowych i ich odpowiedników, a także sporządzimy schematy zgodnie ze wzorami strukturalnymi. Rozważamy również główne obwody logiczne, które pełnią funkcje algebry boolowskiej.

Kontynuacja artykułu: Algebra boolowska. Część 3. Schematy kontaktowe

Boris Aladyshkin