Булева алгебра. Част 3. Схеми за контакт

Статията описва основните принципи за проектиране на релейни вериги в съответствие с даден алгоритъм на тяхната работа.

На две предишни статии беше казано за основите Булева алгебра и реле алгебра, На тази основа са разработени структурни формули и вече са разработени типични контактни вериги.

Съставянето на структурна формула по готова схема е прост въпрос. Много по-трудно е да се представи електрическата верига на бъдещата машина според готовата структурна формула. Нужно е малко обучение!

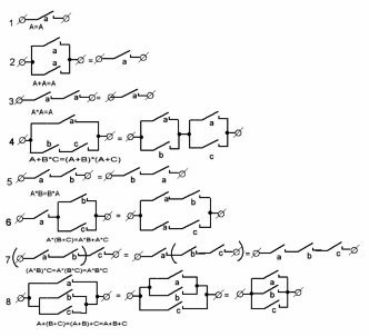
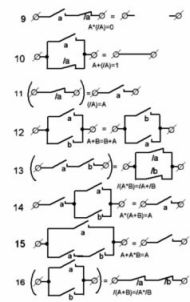
Фигура 1 показва най-често срещаните опции. контактни вериги и техните еквиваленти. Те ще помогнат при подготовката на електрически вериги на машини, както и да анализират готови конструкции, например, в процеса на ремонта им.

Как можете да използвате опциите за контактни вериги, разгледани по-горе?

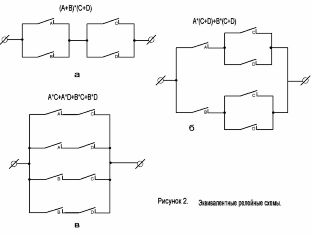
Помислете за схемата, показана на фигура 2, a. Съответната структурна формула има формата: (A + B) * (C + D).

Използвайки закона за разпределение на булева алгебра, отваряме скобите в този израз и получаваме: A * (C + D) + B * (C + D), което съответства на схемата, показана на фигура 2, б. Освен това, благодарение на умножението, можем да получим формулата A * C + A * D + B * C + B * D, съответстваща на фигура 2, c.

И трите схеми са равностойни, тоест те се оказват затворени при еднакви условия. Те обаче са различни по сложност.

Фигура 1. Типични контактни вериги

Първата от веригите, най-простата, изисква четири релета, всяко от които трябва да има един нормално отворен контакт. (За да се опростят чертежите, релейните бобини не са показани).

Схема "b" изисква реле с две контактни групи. Всъщност основната задача на алгебрата на контактните вериги е да намери всички еквивалентни вериги, така че да можете да изберете най-простата от тях.

Фигура 2. Еквивалентни контактни вериги.

За да консолидирате покрития материал, опитайте се сами да решите следните проблеми.

1. Начертайте схемата на автомат със структурна формула A * B * C * D + A * B * E + A * D.

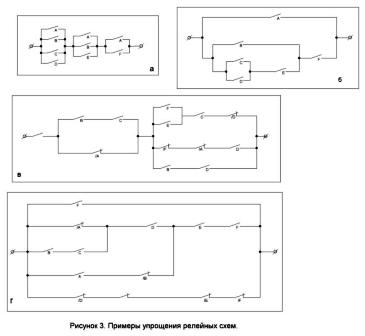
2. Докажете, че схемите, показани на фигура 3, a и b, са еквивалентни.

3. Опростете схемата, показана на фигура 3, в.

4. Каква структурна формула изпълнява схемата на фигура 3, г?

След това, което вече проучихме, ще бъде възможно да започнем да решаваме проблемите, които бяха поставени в самото начало на първата статия. Припомняме ги накратко.

Първата задача беше да включите и изключите електрическата крушка в стаята с три превключвателя, разположени на различни места: на вратата, на масата, на леглото.

Втората задача е да се гласуват спортни съдии: от четирима съдии „ЗА” трябва да гласуват поне двама, при условие че „ЗА” председателят на комисията гласува.

Третата задача беше само за образователни цели. Той предложи същото като в първия, само за шест превключвателя, сякаш в стаята има шест стени. Подобни схеми току-що се разработват с помощта на алгебрата на релейните вериги.

Като цяло, ако искаме да разработим схема, която има някои зададени логически свойства, тогава можем да подходим към този проблем по два различни начина. Обикновено тези пътеки могат да бъдат наречени „интуитивни“ и „алгебраични“.

Някои задачи са по-добре решени по първия начин, докато други по втория. Интуитивният подход се оказва по-удобен, когато работата на веригата се контролира от много превключватели, но има известна симетрия във взаимното подреждане на тези релета. Ще видим, че тук интуитивният подход води по-бързо до целта, докато използването на релейната алгебрална апаратура в случай на много променливи може да бъде много тромаво. Полезно е да се запознаете с двата възможни подхода за решаване на този проблем.

Нека започнем с интуитивен подход. Да предположим, че трябваше да изградим верига, която беше затворена, когато работеха всички n контролни релейни вериги.

Решението на този проблем не изисква дълго обсъждане: ясно е, че зададеното условие ще бъде изпълнено, ако са свързани помежду си последователно n нормално отворени релейни контакти.

По подобен начин е очевидно, че за да се изгради схема, която се затваря, когато поне едно от n релета се е задействало, е достатъчно паралелно да свържете n нормално отворени релейни контакти.

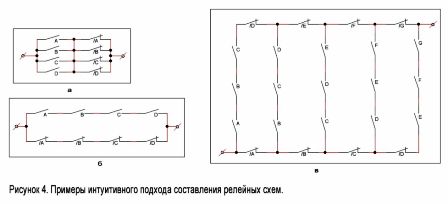
Лесно е да си представим схема, която се затваря, когато се задействат някои, но не всички релета. Такава схема е показана на фигура 4, a. Вдясно е диаграма, която работи на принципа „всичко или нищо“. Той ще бъде затворен само когато всички релета се включат или релетата са изключени (Фигура 4, 6).

Помислете сега за по-сложен пример. Нека има n контакта, разположени в определена специфична последователност: A, B, C, D, E, F ... Ще конструираме верига, която се затваря, когато всички k-свързани контакти са затворени, и само те са. Такава схема за стойностите n = 7 и k = 3 е показана на фигура 4, с. Методът за конструиране на такива схеми за всякакви други стойности на n и k е ясен от тази фигура.

Пристъпваме към изграждането на вериги според дадените условия на тяхната работа, използвайки реле алгебра.

Както преди, условията на работа на веригата винаги винаги се задават устно. На първо място дизайнерът трябва да може да изрази с думи това, което иска. Ако той няма такава яснота, тогава никоя алгебра няма да помогне. Винаги трябва да започнете с ясно изложение на изискванията, които са поставени преди новата схема. Както във всеки бизнес и тази задача е може би най-трудната. Ако условията са достатъчно прости, тогава веднага можем да напишем израз на структурна формула, която удовлетворява тези изисквания.

Пример 1 Да предположим, че трябва да изградим верига, съдържаща 4 контакта A, B, C и D, така че веригата да е включена, когато контакт A е затворен, и един от останалите три контакта. В този прост случай работата на веригата във вербална нотация ще изглежда така: „Веригата трябва да провежда ток, ако контактите A и B са затворени или контактите A и C или контактите A и D. Съгласете се, че сега е много просто да се състави структурна формула. Ще изглежда така:

A * B + A * C + A * D = 1 или A * (B + C + D) = 1.

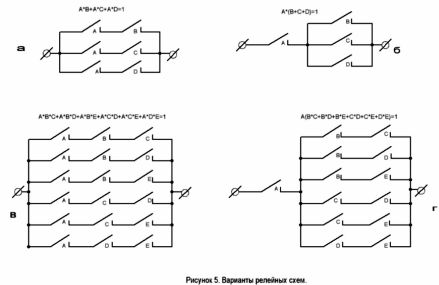
Веригата има две опции. Те са показани на фигура 5. Втората опция не изисква реле с три нормално отворени контакта.

Пример 2 Първата статия беше задача номер 2 относно гласуването на спортните съдии. Прочетете по-отблизо състоянието му, подобно е на току-що разгледания пример. По-ясният словесен запис на изискванията ще изглежда така: „Необходимо е да се състави схема, съдържаща 5 контакта A, B, C, D, E, така че тя да провежда ток и да включва лампата на дисплея, ако следните контакти са затворени:

A и B и C, или A и B и D, или A и B и E, или A и C и D, или A и C и E, или A и D и E. Контактът A е бутонът на председателя. Ако не е натиснато, всеки от 6-те логически продукта ще бъде 0, т.е. Гласуването не се проведе.

Структурната формула ще бъде следната:

(A * B * C) + (A * B * D) + (A * B * E) + (A * C * D) + (A * C * E) + (A * D * E) = 1,

или A * (B * C + B * D + B * E + C * D + C * E + D * E) = 1.

И двата варианта на схемата са показани на фигура 5, в и d. Това е решението на проблема.

Имайки известно умение да чете структурни формули, лесно е да си представим схемата на самия автомат и всички негови възможности. Интересното е, че алгебрата на релейните вериги предоставя повече информация, отколкото дори самата верига. Тя ви позволява да видите колко и кои релета са необходими. С негова помощ можете лесно да намерите най-простата версия на верижната машина.

Пример 3 Натрупайки известен опит в подготовката на структурни формули, ще се опитаме да разрешим започнатия проблем първа статия: трябва да проектирате превключвател, който ви позволява да включите светлината при влизане във входа и да я изключите, след като сте се изкачили на желания етаж, или, обратно, да го включите, когато излизате от апартамента и да го изключвате, след като слезете надолу. Същата ситуация се случва в дълъг коридор: в единия край крушката трябва да бъде запалена, а след като отиде в другия край, да се угаси. Накратко, задачата се свежда до управление на една крушка от различни места с два превключвателя.

Избираме следната процедура за решаване на проблема: първо, ние ясно формулираме работните условия на превключвателите, след това ги записваме под формата на формула и на тях ще изчертаем електрическа верига.

Така че, за да изгори крушката (1), е необходимо едно от двете условия да бъде изпълнено:

1. Включете ключа в долната част (A) и изключете в горната част (/ B). Влез в верандата.

2. Включете превключвателя в горната част (B) и изключете дъното (/ A). Напуснете апартамента.

Използвайки приетата нотация, структурната формула се записва, както следва:

A * (/ B) + (/ A) * B = 1

Схемата на превключвателя е показана на фигура 6. В момента такива превключватели са налични в търговската мрежа, това са т.нар захранващи превключватели, Следователно разглеждането на тези схеми тук е дадено просто за концепцията за общите принципи на тяхната работа.

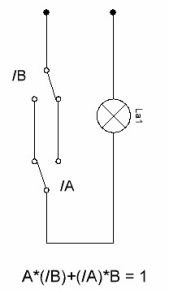
Фигура 6

В задача № 1 в началото на първата статия говорихме за схема, която ви позволява да включите и изключите светлината в стаята с някой от трите превключвателя. Разсъждавайки по същия начин, както в случая на два превключвателя, получаваме структурната формула:

A * B * (/ C) + A * (/ B) + (/ A) * B * C = 1.

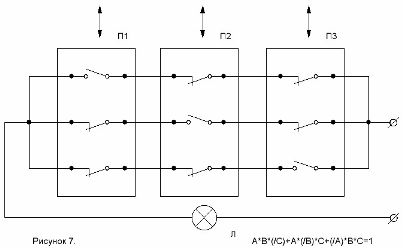
Схемата, изготвена по тази формула, е показана на фигура 7.

Фигура 7

В началото на първата статия е предложена проста образователна задача № 2: сякаш в стаята има шест стени и всяка от тях има превключвател. Логиката на схемата е абсолютно същата като при трите превключвателя. Нека ги обозначим с буквите A, B, C, D, E, F. Спомнете си, че обозначаването (/ A), (/ B) и т.н., това не е знак за разделяне, а логично отрицание. По-често се обозначава с подчертаване на символи и дори цели изрази отгоре. В някои схеми това подчертаване просто се заменя със знак минус. И така, структурната формула за шестте превключвателя е:

(/ A) * B * C * D * E * F + A * (/ B) * C * D * E * F + A * B * (/ C) * D * E * F + A * B * C *

(/ D) * E * F + A * B * C * D * (/ E) * F + A * B * C * D * E * (/ F) = 1.

Читателите се приканват да съставят цялостна електрическа верига, която реализира тази структурна формула, за да придобият практически умения в проектирането на вериги. Малко намек: за веригата ще ви трябват шест релета, всяко от които има един нормално отворен контакт и пет нормално затворени. Такива сложни релета, ако е необходимо, могат да бъдат сглобени от няколко по-прости, като се свържат паралелно техните бобини.

С това завършва историята за булева алгебра и алгебрата на релейните вериги.

Продължение на статията: Логически чипове

Борис Аладишкин