Булева алгебра. Част 2. Основни закони и функции

Продължение на историята за булева алгебра, конвенции, правила, операции. Преход към основите на контактните вериги.

Най- първа статия Джордж Бул беше описан като създател на алгебрата на логиката. Втората статия ще опише основните операции на булева алгебра и методите за опростяване на булевите изрази. И така, булева алгебра използва изявления като аргументи и не тяхното значение, а истинността или лъжливостта на твърдението.

Формата за писане на изрази в булева алгебра.

Ако твърдението е вярно, тогава се пише така: A = 1, ако е невярно, тогава A = 0 (в края на краищата не е вярно, че картофът е плод). За всяко твърдение A е или вярно (A = 1), или невярно (A = 0). Тук не може да има средата. Вече говорихме за това.

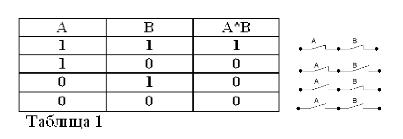
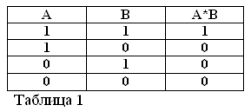
Ако свържете две прости операции с обединението И, получавате сложно изявление, което се нарича логичен продукт. Да вземем две прости твърдения: „Три е повече от две“ ще обозначим с буква А, „Три по-малко от пет“ - с буква Б.

Следователно сложната поговорка „Три е повече от две И по-малко от пет“ е логична (в случая главната буква I обозначава, че това е логическа операция „И“, както и по-късно в текста „ИЛИ“ и „НЕ.“) и Б. Той е обозначен както следва: A ^ B или A * B.

Логическо умножение (операция "И").

В елементарната алгебра A * A = A2. Но в алгебрата на Бул A * A = A2 = A, A * A = A, тъй като знакът за умножение (*) сега означава ... И ... в смисъла на И ... И. Целият наш опит потвърждава, че A&A е същото като А. Само че не може да не се съглася с това. Истинността на твърдението не се променя, ако се повтори от фактора няколко пъти.

Продуктът от две твърдения се счита за истина (равен на 1), тогава и само ако и двата фактора са верни, и неверни (равни на 0), ако поне един от факторите е невярен. Съгласете се, че тези правила не противоречат на здравия разум и освен това напълно спазват правилата на елементарната алгебра:

1*1 = 1, 1*0 = 0 = 0*1 = 0, 0*0 = 0.

Първото равенство гласи следното: ако и A, и B са верни, тогава продуктът A * B е истина. В алгебрата на Бул знакът за умножение (*) замества съединението I.

Логическите продукти могат да включват не две, а по-голям брой твърдения - фактори. И в този случай продуктът е валиден само когато в същото време всички твърдения-фактори са верни.

Логическо допълнение (ИЛИ операция)

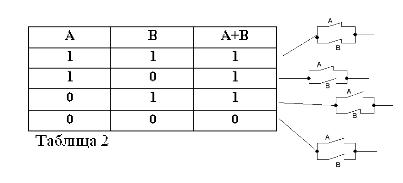
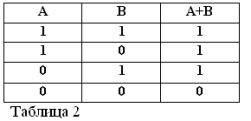
Ако две изявления са свързани от съюз ИЛИ. това образувано съставно изречение се нарича логическа сума.

Помислете за пример на логическа сума. Казвайки А: „Днес ще отида на кино“.

Изявление Б: „Днес ще отида на дискотека.“ Добавяме и двете твърдения и получаваме: „Днес ще отида на кино ИЛИ на дискотека“.

Това сложно изложение се обозначава по следния начин: A + B = C или (A V B) = C.

С C обозначихме сложно изложение на логическа сума.

В разглеждания пример съюзът ИЛИ не може да се използва в изключителен смисъл. Наистина, в същия ден можете да стигнете до киното и до дискотеката. И ето поговорката:

„Председател на партньорството за градинарство ще бъде Петров или Иванов“, не е логична сума, тъй като само един човек ще бъде председател, а другият ще бъде любителски обикновен градинар.

Знакът V за логическата сума е избран, защото е началната буква на латинската дума „vel“, което означава „или“, за разлика от латинската дума „aut>, което означава„ и “. Сега трябва да е ясно на всички защо логичният продукт е обозначен със знака ^.

В елементарната алгебра има правило A + A = 2A. Това правило е вярно, без значение кое число е представено с буквата А. В булева алгебра правилото A + A = A. съответства на него. Целият ни житейски опит казва, че да кажеш A OR A или и двете A е просто друг и по-дълъг начин да кажеш просто A.

Както всяко сложно твърдение, сборът от двете твърдения A и B може да бъде вярно или невярно. Сумата се счита за вярна, тоест равна на единство, ако поне един от термините е истина:

A + B = 1, ако OR A = 1 OR B = 1, което е в съответствие с конвенционалната аритметика:

1+0 = 0+1 = 1.

Ако и двете обобщени твърдения са верни, тогава сумата също се счита за вярна, следователно в булева алгебра имаме: (1) + (1) = 1.

Тук скобите са зададени, за да се подчертае условното, значението на това допълнение, а не аритметиката.

Сумата от две твърдения се счита за невярна и равна на нула, ако, но само ако и двата термина са неверни. От тук:

0 + 0=0.

И така, сумата от двата твърдения A + B се счита за вярна, ако е вярна, ИЛИ А, ИЛИ Б, ИЛИ и двете термини заедно. Така думата ИЛИ се обозначава със знака +.

Помнете, че изявленията А и В могат да бъдат само верни или неверни и следователно да имат мярка за истина 1 или 0, резултатите от разглежданите операции И и ИЛИ могат да бъдат обобщени в таблици 1 и 2.

Третата операция, широко използвана от алгебрата Бул, е операцията за отрицание - НЕ. Припомняме ви, че елементарната алгебра използва операциите ADD, D изваждане, умножение по, разделяне и някои други.

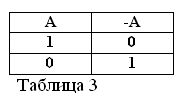
За всяко твърдение А има своето отрицание НЕ А, което ще обозначим със символа / А. Това не трябва да е под въпрос.

Даваме примери: „Ще отидем в гората“ A, „Няма да отидем в гората“ / A.

Ако твърдението A е вярно, тоест A = 1, тогава неговото отрицание / A трябва да бъде невярно / A = 0. И обратно, ако някое твърдение е невярно, тогава отрицанието му е вярно. Например: „Кон не яде сено“ / A = 0, „Кон не яде сено“ (A = 1). Това може да се изрази в таблица 3.

Определяйки значението на действието на отрицанието и приемайки, че от двете твърдения A и / A винаги е една истина, следват две нови формули на булева алгебра:

A + (/ A) = 1 и A * (/ A) = 0.

Има и други формули, които опростяват логическата обработка на изявленията. Например 1 + A = 1, тъй като според дефиницията на добавянето, в случаите, когато един член е равен на единство, сумата винаги е равна на единица. Полученият резултат не зависи от това дали A = 0 или A = 1.

Всяка от трите логически операции, които разгледахме (И, ИЛИ, НЕ) има определени свойства, близки до правилата на елементарната алгебра. Ако всички те са формулирани, тогава получаваме 25 правила на булева алгебра. Те са напълно достатъчни, за да решат почти всеки логически проблем. Без тези правила става доста трудно да се решат логически проблеми поради очевидната им сложност. Опитът да намерите правилния отговор без да използвате правилата означава да ги замените с изобретателност и общи разсъждения. Правилата значително улесняват тази работа и спестяват време.

В рамките на статията е невъзможно да се разгледат всички тези 25 правила, но желаещите винаги могат да ги намерят в съответната литература.

Както вече беше споменато в първата статия през 1938 г., младият американски учен Клод Шенън в своята статия „Символичен анализ на релейни и комутационни вериги“ за първи път използва булева алгебра за проблеми на релейната технология. Откритието на Шанън беше, че той осъзна, че методът за проектиране на релейни машини и електронни компютри всъщност е клон на математическата логика.

Често се случва. Дълги години ученият работи по проблем, който изглежда напълно ненужен за сънародниците му - просто забавление. Но минават десетилетия и понякога векове, а теория, от която никой не се нуждае, не само придобива правото на съществуване, но и без него по-нататъшният напредък става немислим.

Какво помогна на Шанън втори път да открие булева алгебра? Случаят? Нищо подобно.

Любовта към релейните машини, изградени на конвенционални превключватели и релета, помогна на младия учен да свърже забравена теория със задачите на автоматичните телефонни станции, върху които той работи по това време. По-късно Шанън въведе същата идея за „да или не“ в дискретни послания и постави основата на цял раздел от кибернетиката - теория на информацията.

Алгебрата на Бул беше много подходяща за анализ и синтез на релейни вериги. Беше достатъчно да приемем като вярно твърдение: „В схемата има сигнал“, а като невярно - „Няма сигнал във веригата“, тъй като се появи нова алгебра - сигналната алгебра, алгебрата на релейната верига.

Новата алгебра е валидна само за разглеждане на релейни и комутационни вериги. Всъщност само в такива схеми е изпълнено условието „има сигнал“ и „няма сигнал“. Когато сигналът се променя непрекъснато, придобивайки произволно голям брой междинни условия (такъв сигнал се нарича аналогов), релейната алгебра не е приложима. Това винаги трябва да се помни. Но само повечето електронни компютри и кибернетични машини използват дискретен принцип на обработка на сигнала, който се основава на елементите „да - не“.

Изразът „Контактът е затворен“ беше приет от Шанън като верен (1), а „Контакт отворен“ като невярен (0). Останалата част от "алгебрата", включително операциите И, ИЛИ и НЕ, и 25 правила, Шанън заимства от Бул.

Алгебрата на релейната верига се оказа по-проста от булева алгебра, тъй като се занимава само с елементи от типа да-не. Освен това новата алгебра е по-визуална.

Елементите в тази алгебра са контактите, които ще обозначим с буквите A, B, C ... Контактът е затворен - A, контактът е отворен - / A (буква с тире).

Обозначението, както виждате, е изцяло взето от булева алгебра. Отворен контакт е отрицание на затворен контакт. Един и същ контакт не може да бъде затворен и отворен.

Съгласни сме, че ако във всяка схема два контакта са обозначени с една и съща буква, тогава това означава, че те винаги приемат едни и същи стойности.

Във всеки даден момент те са или отворени едновременно, или и двете са затворени. Най-лесният начин да си ги представите механично свързани заедно, така че и двамата едновременно да се отварят или затварят.

Ако в някоя верига контактът е отрицание на друг контакт, значенията им винаги са противоположни. Например контактите C и / C никога не могат да бъдат едновременно отворени или едновременно затворени. И в диаграмата те могат да бъдат представени механично свързани: ако единият от тях се отвори, тогава другият се затваря.

Започваме запознаването ни с релейната алгебра, като анализираме най-простите схеми, съответстващи на операциите AND, OR и NOT.

Продуктът от два контакта (операция И) е веригата, получена в резултат на тяхното последователно свързване: тя се затваря (равна на 1), само когато и двата контакта са затворени (равни на 1).

Сумата от два контакта (ИЛИ операция) ще бъде схемата, образувана, когато са свързани паралелно: тя е затворена (равна на 1), когато поне един от контактите, образуващи веригата, е затворен (равен на 1).

Обратното на този контакт (операция НЕ) е контакт, равен на 0 (отворен), ако този контакт е 1 (затворен), и обратно.

Както в булевата алгебра, ако контактите са обозначени с буквите A и B, тогава произведението на два контакта ще обозначим с A * B, сумата с A + B и контакта срещу A, с / A. Горното е обяснено на фигури 1, 2 и 3.

Валидност на таблиците, съответстващи на операции AND, OR и NOT. сега никой не трябва да се съмнява.

Нека се спрем на два примера: 1 * 0 = 0 и 1 + 0 = 1.

От фигурата се вижда, че постоянно затворен контакт, свързан последователно с постоянно отворен контакт, е еквивалентен на постоянно отворен контакт (1 * 0 = 0) Постоянно затворен контакт, свързан успоредно с постоянно отворен контакт, е еквивалентен на постоянно затворен контакт.

След като се запознаете с аритметиката на контактните вериги, можете да опишете всяка релейна верига с формула, като използвате приетите конвенции. В кибернетиката такива формули се наричат ​​структурни.

Ако структурната формула на която и да е релейна верига е 1, тогава през нея може да премине сигнал - веригата е затворена. И обратно, ако структурната формула на веригата е 0, сигналът няма да премине през нея - веригата е прекъсната.Заключение: две релейни вериги са еквивалентни една на друга, когато техните структурни формули са равни.

В продължение на статията ще разгледаме примери за контактни вериги, типични контактни вериги и техните еквиваленти, както и изготвяне на диаграми според структурни формули. Ние също така разглеждаме основните логически схеми, които изпълняват функциите на булева алгебра.

Продължение на статията: Булева алгебра. Част 3. Схеми за контакт

Борис Аладишкин