Булева алгебра. Част 1. Малко история

В училище всички изучавахме алгебра, но там не говориха за булева алгебра. Каква е разликата между булева алгебра и училищна алгебра, историята на нейното появяване, проблеми и приложения са описани в тази статия.

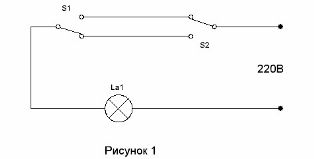
Веригата, която позволява на два ключа да включи светлината в коридора на входа на коридора и да го изключи при влизане в стаята, е позната от много отдавна (виж. Контролна верига за осветление на коридора). Тя е показана на фигура 1.

Задача номер 1, По-сложно. Създайте схема, която ви позволява да включвате и изключвате светлината в стаята си с който и да е от 3 различни превключвателя. Превключвателите са разположени на входа на стаята, над леглото и на бюрото.

Задача номер 2.

В спортен комитет, като фабрична комисия, се събраха 5 съдии.

Всеки от тях трябва да гласува за различни решения. Решението се приема с мнозинство гласове, но само при допълнително условие председателят на комисията да гласува за него.

Съдиите гласуват с натискане на бутона, който затваря превключвателя, разположен под масата, на която седят. Затваряйки превключвателя, те гласуват „за“, изключвайки минусите. Начертайте проста схема, която ви позволява автоматично да виждате резултатите от гласуването. В най-простия случай, просто с помощта на крушка - запалена - решението е взето, не светна - не.

Задача номер 3, На практика това е малко вероятно, но като сложна образователна задача е доста подходяща.

В голямо шестоъгълно помещение е поставен по един превключвател на всяка стена. Изградете схема, така че по всяко време да можете да включите или изключите светлината в стаята, като завъртите един (произволен) превключвател.

След като безуспешно седнете над задачи в продължение на три до четири дни, заделете ги временно. И се заемете Булева алгебра, Това е булева алгебра или, както се нарича още, Булева алгебра, алгебра с релейна верига, ще ви помогне да решите проблемите си.

Какво е булева алгебра?

Колкото и да е странно, въпреки факта, че в продължение на пет години учат алгебра в училище, много ученици, а по-късно и възрастни, няма да могат да отговорят на въпроса какво е алгебра? Алгебра е наука, която изучава наборите на някои елементи и действията върху тях.

В училищен курс по алгебра такива елементи са числа. Числата могат да се означават не с цифри, а с букви, всеки е запознат с това. В първите уроци по алгебра това винаги затруднява много ученици. Спомнете си колко беше трудно в началото да свикнете да сгъвате букви вместо цифри, да решавате уравнения, които не казват нищо.

Вероятно след това всеки от нас си зададе въпроса: „Защо трябва да въвеждаме букви вместо цифри и това изобщо е необходимо?“ И едва по-късно видяхте какви предимства дава алгебрата при решаване на задачи в сравнение с аритметика.

Алгебрата се използва в много точни науки. Това е физика, механика, сопромат, електричество. Закон на Ом няма нищо повече от алгебрично уравнение: достатъчно е да заменим техните числови стойности вместо букви, за да разберем какъв ток ще тече в товара или какво съпротивление има една секция от веригата.

Така се запознахте с алгебрата на числата или с елементарната алгебра. Основната и почти уникална задача е да получите отговор на въпроса: „На кое е X равно? Колко? “

В гимназията изучават наченките на векторната алгебра. Тази алгебра е коренно различна от елементарната алгебра. Тя има различно естество на изследвания набор и други правила на действие. Решавайки векторното уравнение, получаваме в отговора вектор, който не е обикновено число, което отговаря на въпроса "Колко?"

Формулите на векторната алгебра в много отношения се различават от формулите на елементарната алгебра. Например в елементарната алгебра и във векторната алгебра има операция за добавяне. Но тя се изпълнява по съвсем различни начини.Добавянето на числа изобщо не е същото като добавянето на вектори.

Има и други алгебри: линейна алгебра, алгебра от структури, алгебра на пръстените, алгебра на логиката или, което е същото, булева алгебра. Вероятно не сте чували името в уроците в училище. Джордж Бул - но всички знаят името на една от талантливите му дъщери Етел Войнич (1864 - 1960). Тя написа романа „Gadfly“, който говори за борбата за правата на италианските карбонари.

Джордж Бул е роден в Англия на 2 ноември 1815 г. Цял живот работи като учител по математика и физика в училище. От спомените на неговите ученици се знае какво голямо значение Бул придава на развитието на творческите способности на учениците. Представяйки нов материал, той се стреми да гарантира, че неговите ученици сами „преоткриват“ определени формули и закони.

Разказвайки на учениците за трудностите, с които учените неизбежно се сблъскват в търсенето на истината, учителят обичаше да повтаря една източна мъдрост: дори персийският трон не може да донесе толкова много удоволствие на човек, колкото най-малкото научно откритие. Бул никога не е губил надежда, че някой ден неговите ученици ще направят истинско откритие.

Обхватът на научните интереси на Бул беше много широк: той еднакво се интересуваше от математиката и логиката - науката за законите и формите на мислене. В онези дни логиката се смяташе за наука за хуманитарните науки и мнозина, които познаваха Джордж Бул, бяха изумени как точните методи на познание, присъщи на математиката, и чисто описателните методи на логиката могат да съществуват в един човек.

Но ученият искаше да направи науката за законите и формите на мислене толкова строга, колкото всяка една от естествените науки, да речем математиката и физиката. За това Бул започна да обозначава не цифри като букви, както се прави в обикновената алгебра, а изявления и показа, че подобни уравнения, много подобни на алгебричните, могат да решават въпроси за истинността и лъжливостта на твърденията, направени от човека. Така възникна Булевата алгебра.

Но много преди Джордж Бул германският математик и философ Готфрид Лайбниц (1646-1716) за пръв път излезе с идеята да създаде наука, която да обозначи всички понятия на обикновената разговорна реч със символи и да създаде нова алгебра за комбиниране на тези символи.

След създаването на такава наука, според Лайбниц, учените и философите ще спрат да спорят и да викат един на друг, да разберат истината, но ще вземат молив и спокойно ще кажат: „Нека изчислим!“

Днес алгебрата на логиката се превърна във важна част от математиката. Една от задачите му е да решава всички видове уравнения, числените съотношения на които се заменят с азбучни. Всеки от вас вероятно през целия си живот си спомня как да решава уравнения от втора и трета степен с буквен коефициент. И така, Бул в новата си алгебра използва всички тези формули и правила.

Новото в булева алгебра е, че елементите от множеството, които се изучават в нея, не са числа, а твърдения. Ако при решаването на обикновени алгебрични уравнения се определи кое число е равно на неизвестно X, училищната алгебра търси отговора на въпроса: "Колко?"

Алгебрата на логиката търси отговора на въпроса: „Вярно ли е това или онова изявление, обозначено с буквата X?“

Значението и съдържанието на изявлението не играят никаква роля тук. Всяко твърдение може да бъде само вярно или невярно. Не може да бъде наполовина вярно и наполовина невярно. Като пример можем да си припомним хвърлянето на партиди с монета.

Там се разглеждат само две състояния на монети - глави или опашки. По споразумение на страните, орелът е ДА, а опашките НЕ са. Никакви други междинни точки не се вземат предвид при теорията на вероятностите, въпреки че са възможни. Една обърната монета може да падне на ръба, да се търкаля по пода до краката на стол или маса и да остане в изправено положение или дори да падне в широка празнина в пода. (По аналогия с електрическите вериги, последните две ситуации могат да се считат за неизправност под формата на изгорял контакт).Но в онези дни булева алгебра, уви, не се използва широко.

Клод Шенън отново „откри“ алгебрата Бул. През 1938 г., още като студент в Масачузетския технологичен институт и Америка, младият Клод доказва, че булева алгебра е напълно подходяща за анализ и синтез на релейни и комутационни вериги.

С помощта на булева алгебра е много лесно да се направи електрическа верига на релейна машина.За това, оказва се, трябва само да знаете какво точно трябва да прави машината, тоест трябва да имате алгоритъм за нейната работа. Така основата беше поставена за теорията на цифровите машини, работещи на принципа ДА или НЕ.

Такава, накратко, е историята на булева алгебра. В следващите статии ще разгледаме основните му закони, примери за контактни вериги, прилагащи тези закони. Помислете за решението на онези задачи, които бяха дадени в началото на статията.

Продължение на статията: Булева алгебра. Част 2. Основни закони и функции

Борис Аладишкин