Algèbre booléenne. Partie 2. Lois et fonctions de base

Suite de l'histoire de l'algèbre booléenne, des conventions, des règles, des opérations. Transition vers les bases des circuits de contact.

Dans premier article George Bull a été décrit comme le créateur de l'algèbre de la logique. Le deuxième article décrira les opérations de base de l'algèbre booléenne et les méthodes de simplification des expressions booléennes. Ainsi, l'algèbre booléenne utilise des déclarations comme arguments, et non leur signification, mais la vérité ou la fausseté de la déclaration.

La forme pour écrire des expressions en algèbre booléenne.

Si l'énoncé est vrai, alors il est écrit comme ceci: A = 1, s'il est faux, alors A = 0 (après tout, ce n'est pas vrai que la pomme de terre est un fruit). Pour toute déclaration, A est vrai (A = 1) ou faux (A = 0). Il ne peut pas y avoir de milieu ici. Nous en avons déjà parlé.

Si vous connectez deux instructions simples à l'union And, vous obtenez une instruction complexe, qui est appelée un produit logique. Prenons deux expressions simples: «Trois, c'est plus de deux», nous désignerons par la lettre A, «Trois moins de cinq» - par la lettre B.

Par conséquent, l'énoncé complexe «Trois est plus de deux et moins de cinq» est logique (dans ce cas, la lettre majuscule Et, dit que c'est une opération logique «ET», ainsi que plus loin dans le texte «OU» et «NON»). et B. Il est désigné comme suit: A ^ B ou A * B.

Multiplication logique (opération "ET").

En algèbre élémentaire A * A = A2. Mais dans l'algèbre de Buhl A * A = A2 = A, A * A = A, puisque le signe de multiplication (*) signifie maintenant ... Et ... dans le sens de Et ... Et. Toute notre expérience confirme que A&A est la même chose que A. seul. On ne peut pas être en désaccord avec cela. La vérité de l'énoncé ne change pas si elle est répétée plusieurs fois par le facteur.

Le produit de deux déclarations est alors considéré comme vrai (égal à 1), et seulement si les deux facteurs sont vrais, et faux (égal à 0) si au moins l'un des facteurs est faux. Convenez que ces règles ne contredisent pas le bon sens et, en outre, elles respectent pleinement les règles de l'algèbre élémentaire:

1*1 = 1, 1*0 = 0 = 0*1 = 0, 0*0 = 0.

La première égalité se lit comme suit: si A et B sont vrais, alors le produit A * B est vrai. Dans l'algèbre de Buhl, le signe de multiplication (*) remplace l'union I.

Les produits logiques peuvent comprendre non pas deux, mais un plus grand nombre de déclarations - facteurs. Et dans ce cas, le produit n'est vrai que si en même temps tous les facteurs-énoncés sont vrais.

Addition logique (opération OR)

Si deux relevés sont reliés par un syndicat OU. cette phrase composée formée est appelée une somme logique.

Prenons un exemple de somme logique. Dire A: "Aujourd'hui, j'irai au cinéma."

Déclaration B: "Aujourd'hui, je vais à la discothèque." Nous ajoutons les deux déclarations et obtenons: "Aujourd'hui, j'irai au cinéma OU dans une discothèque."

Cette déclaration complexe est notée comme suit: A + B = C ou (A V B) = C.

Par C, nous avons noté un énoncé complexe d'une somme logique.

Dans l'exemple considéré, l'union OR ne peut pas être utilisée dans un sens exclusif. En effet, le même jour, vous pouvez vous rendre au cinéma et à la discothèque. Et voici le dicton:

«Le président du partenariat de jardinage sera Petrov ou Ivanov», ce n'est pas une somme logique, car une seule personne sera le président, et l'autre sera un jardinier amateur ordinaire.

Le signe V pour la somme logique est choisi car il s'agit de la lettre initiale du mot latin "vel", qui signifie "ou", contrairement au mot latin "aut>, qui signifie" et ". Maintenant, il devrait être clair pour tout le monde pourquoi le produit logique est indiqué par le signe ^.

En algèbre élémentaire, il existe une règle A + A = 2A. Cette règle est vraie, quel que soit le nombre représenté par la lettre A. Dans l'algèbre booléenne, la règle A + A = A correspond à cela. Notre expérience de vie entière dit que dire A OU A ou les deux A est juste un autre et plus long moyen de dire juste A.

Comme toute déclaration composée, la somme des deux déclarations A et B peut être vraie ou fausse. La somme est considérée comme vraie, c'est-à-dire égale à l'unité, si au moins un des termes est vrai:

A + B = 1 si OU A = 1 OU B = 1, ce qui est conforme à l'arithmétique conventionnelle:

1+0 = 0+1 = 1.

Si les deux déclarations sommées sont vraies, alors la somme est également considérée comme vraie, par conséquent, dans l'algèbre booléenne, nous avons: (1) + (1) = 1.

Les parenthèses sont définies ici afin de souligner le conditionnel, la signification de cet ajout et non l'arithmétique.

La somme de deux déclarations est considérée comme fausse et égale à zéro si, mais seulement si les deux termes sont faux. D'ici:

0 + 0=0.

Ainsi, la somme des deux énoncés A + B est considérée comme vraie si elle est vraie, OU A, OU B, OU les deux termes ensemble. Ainsi, le mot OU est noté +.

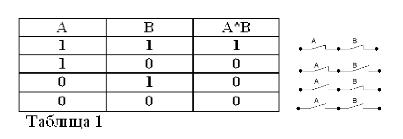
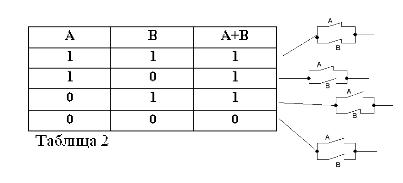
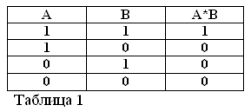
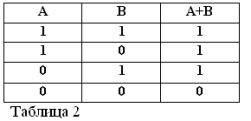
En se rappelant que les déclarations A et B ne peuvent être vraies ou fausses et, par conséquent, avoir une mesure de vérité 1 ou 0, les résultats des opérations ET et OU considérées peuvent être résumés dans les tableaux 1 et 2.

La troisième opération, largement utilisée par l'algèbre de Buhl, est l'opération de négation - NON. Nous vous rappelons que l'algèbre élémentaire utilise les opérations ADD, D Subtract, Multiply by, Divide by et quelques autres.

Pour chaque énoncé A, il y a sa négation NON A, que nous désignerons par le symbole / A. Cela ne devrait pas faire de doute.

Nous donnons des exemples: «Nous irons dans la forêt» A, «Nous n'irons pas dans la forêt» / A.

Si la déclaration A est vraie, c'est-à-dire A = 1, alors sa négation / A doit être fausse / A = 0. Et vice versa, si une déclaration est fausse, alors sa négation est vraie. Par exemple: «Un cheval ne mange pas de foin» / A = 0, «Un cheval ne mange pas de foin» (A = 1). Cela peut être exprimé dans le tableau 3.

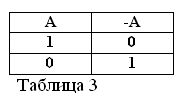
Pour déterminer le sens de l'action de négation, et en supposant que des deux énoncés A et / A soit toujours une vraie, deux nouvelles formules de l'algèbre booléenne suivent:

A + (/ A) = 1 et A * (/ A) = 0.

Il existe également d'autres formules qui simplifient le traitement logique des instructions. Par exemple, 1 + A = 1, puisque, selon la définition de l'addition, dans le cas où un terme est égal à l'unité, la somme est toujours égale à l'unité. Le résultat obtenu ne dépend pas de savoir si A = 0 ou A = 1.

Chacune des trois opérations logiques que nous avons examinées (ET, OU, NON) possède certaines propriétés qui sont proches des règles de l'algèbre élémentaire. Si tous sont formulés, nous obtenons alors 25 règles d'algèbre booléenne. Ils sont suffisants pour résoudre presque tous les problèmes logiques. Sans ces règles, il devient assez difficile de résoudre des problèmes logiques en raison de leur apparente complexité. Essayer de trouver la bonne réponse sans utiliser les règles signifie les remplacer par l'ingéniosité et le raisonnement général. Les règles facilitent grandement ce travail et font gagner du temps.

Dans le cadre de l'article, il est impossible de considérer l'ensemble de ces 25 règles, mais ceux qui le souhaitent peuvent toujours les retrouver dans la littérature pertinente.

Comme déjà mentionné dans le premier article de 1938, le jeune scientifique américain Claude Shannon dans son article «Analyse symbolique des circuits de relais et de commutation» utilise pour la première fois l'algèbre de Boole pour des problèmes de technologie de relais. La découverte de Shannon a été qu'il a réalisé que la méthode de conception de machines relais et d'ordinateurs électroniques est en fait une branche de la logique mathématique.

Cela arrive souvent. Depuis de nombreuses années, le scientifique travaille sur un problème qui semble complètement inutile à ses compatriotes - juste amusant. Mais des décennies et parfois des siècles passent, et une théorie dont personne n'a besoin n'acquiert non seulement le droit d'exister, mais sans elle, de nouveaux progrès deviennent impensables.

Qu'est-ce qui a aidé Shannon à "découvrir" une deuxième fois l'algèbre booléenne? Affaire? Rien de tel.

L'amour des relais, construits sur des interrupteurs et relais conventionnels, a aidé le jeune scientifique à relier une théorie oubliée aux tâches des centraux téléphoniques automatiques, sur lesquels il travaillait à l'époque. Par la suite, Shannon a introduit la même idée de «oui ou non» dans des messages discrets et a jeté les bases d'une section entière de la cybernétique - la théorie de l'information.

L'algèbre de Buhl était très appropriée pour l'analyse et la synthèse des circuits de relais. Il suffisait d'accepter comme une vraie déclaration: "Il y a un signal dans le circuit", et comme faux - "Il n'y a pas de signal dans le circuit", comme une nouvelle algèbre est apparue - l'algèbre des signaux, l'algèbre du circuit relais.

La nouvelle algèbre n'est valable que pour la prise en compte des circuits de relais et de commutation. Après tout, ce n'est que dans de tels schémas que la condition «il y a un signal» et «aucun signal» est satisfaite. Lorsque le signal change continuellement, acquérant un nombre arbitrairement élevé de conditions intermédiaires (un tel signal est appelé analogique), l'algèbre de relais n'est pas applicable. Il faut toujours s'en souvenir. Mais juste la majorité des ordinateurs électroniques et des machines cybernétiques utilisent le principe discret du traitement du signal, qui est basé sur les éléments «oui - non».

L'expression «Contact fermé» a été acceptée par Shannon comme vraie (1) et «Contact ouvert» comme fausse (0). Le reste de "l'algèbre", y compris les opérations ET, OU et NON et 25 règles, Shannon a emprunté à Boole.

L'algèbre du circuit de relais s'est avérée plus simple que l'algèbre de Boole, car elle ne traite que des éléments de type «oui - non». De plus, la nouvelle algèbre est plus visuelle.

Les éléments de cette algèbre sont les contacts, que nous désignerons par les lettres A, B, C ... Le contact est fermé - A, le contact est ouvert - / A (lettre avec un tiret).

La notation, comme vous le voyez, est entièrement empruntée à l'algèbre booléenne. Un contact ouvert est une négation d'un contact fermé. Le même contact ne peut pas être à la fois fermé et ouvert.

Convenons que si dans n'importe quel circuit deux contacts sont désignés par la même lettre, cela signifie qu'ils prennent toujours les mêmes valeurs.

À tout moment, ils sont tous deux ouverts en même temps, ou les deux sont fermés. Le moyen le plus simple de les imaginer reliés mécaniquement les uns aux autres afin que les deux s'ouvrent ou se ferment simultanément.

Si dans une chaîne un contact est la négation d'un autre contact, alors leurs significations sont toujours opposées. Par exemple, les contacts C et / C ne peuvent jamais être ouverts ou fermés simultanément. Et dans le diagramme, ils peuvent être représentés connectés mécaniquement: si l'un d'eux s'ouvre, alors l'autre se ferme.

Nous commençons notre connaissance de l'algèbre de relais en analysant les circuits les plus simples correspondant aux opérations ET, OU et NON.

Le produit de deux contacts (opération ET) est le circuit obtenu grâce à leur connexion en série: il n'est fermé (égal à 1) que lorsque les deux contacts sont fermés (égal à 1).

La somme de deux contacts (fonctionnement OR) sera le circuit formé lorsqu'ils sont connectés en parallèle: il est fermé (égal à 1) lorsqu'au moins un des contacts formant le circuit est fermé (égal à 1).

L'opposé de ce contact (opération NON) est un contact égal à 0 (ouvert) si ce contact est 1 (fermé), et inversement.

Comme dans l'algèbre booléenne, si les contacts sont désignés par les lettres A et B, alors nous désignerons le produit de deux contacts par A * B, la somme par A + B et le contact opposé A, par / A. Ce qui précède est expliqué dans les figures 1, 2 et 3.

Validité des tables correspondant aux opérations AND, OR et NOT. maintenant, personne ne devrait avoir de doute.

Arrêtons-nous sur deux exemples: 1 * 0 = 0 et 1 + 0 = 1.

On peut voir sur la figure qu'un contact fermé en permanence connecté en série avec un contact ouvert en permanence équivaut à un contact ouvert en permanence (1 * 0 = 0) Un contact fermé en permanence connecté en parallèle avec un contact ouvert en permanence équivaut à un contact fermé en permanence.

Une fois familiarisé avec l'arithmétique des circuits de contact, vous pouvez décrire tout circuit de relais avec une formule en utilisant les conventions acceptées. En cybernétique, ces formules sont appelées structurelles.

Si la formule structurelle d'un circuit de relais est 1, un signal peut le traverser - le circuit est fermé. Inversement, si la formule structurelle du circuit est 0, le signal ne le traversera pas - le circuit est rompu.Conclusion: deux circuits relais sont équivalents lorsque leurs formules structurelles sont égales.

Dans la suite de l'article, nous examinerons des exemples de circuits de contact, des circuits de contact typiques et leurs équivalents, ainsi que l'élaboration de schémas selon des formules structurelles. Nous considérons également les principaux circuits logiques qui remplissent les fonctions d'algèbre booléenne.

Suite de l'article: Algèbre booléenne. Partie 3. Schémas de contact

Boris Aladyshkin