Booleovská algebra. Část 3. Kontaktní schémata

Článek popisuje základní principy navrhování reléových obvodů v souladu s daným algoritmem jejich činnosti.

Ve dvou předchozí články bylo řečeno o základech Booleovská algebra a reléová algebra. Na tomto základě byly vyvinuty strukturní vzorce a na nich byly vyvinuty již typické kontaktní obvody.

Vypracování strukturního vzorce podle hotového schématu je jednoduchá záležitost. Je mnohem obtížnější představit elektrický obvod budoucího stroje podle hotového strukturního vzorce. Vyžaduje to nějaké školení!

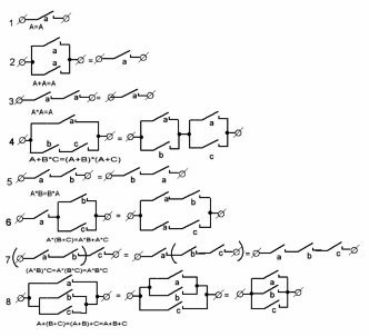
Obrázek 1 ukazuje nejběžnější možnosti. kontaktní obvody a jejich ekvivalenty. Pomohou při přípravě elektrických obvodů strojů, jakož i při analýze hotových struktur, například při jejich opravě.

Jak můžete využít výše uvedené možnosti kontaktních obvodů?

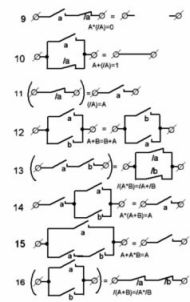
Zvažte obvod zobrazený na obrázku 2, Odpovídající strukturní vzorec má tvar: (A + B) * (C + D).

Pomocí distribučního zákona Booleovské algebry otevřeme závorky v tomto výrazu a dostaneme: A * (C + D) + B * (C + D), což odpovídá schématu znázorněnému na obrázku 2, b. Dále, díky násobení, můžeme získat vzorec A * C + A * D + B * C + B * D, odpovídající obrázku 2, c.

Všechny tři systémy jsou rovnocenné, to znamená, že se ukáže, že jsou uzavřeny za stejných podmínek. Jsou však složité.

Obrázek 1. Typické kontaktní obvody

První z obvodů, nejjednodušší, vyžaduje čtyři relé, z nichž každé musí mít jeden normálně otevřený kontakt. (Pro zjednodušení výkresů nejsou reléové cívky zobrazeny).

Schéma "b" vyžaduje relé se dvěma skupinami kontaktů. Ve skutečnosti je hlavním úkolem algebry kontaktních obvodů najít všechny ekvivalentní obvody, abyste si z nich mohli vybrat nejjednodušší.

Obrázek 2. Rovnocenné kontaktní obvody.

Chcete-li konsolidovat pokrytý materiál, zkuste vyřešit následující problémy sami.

1. Nakreslete schéma zapojení automatu, který má strukturní vzorec A * B * C * D + A * B * E + A * D.

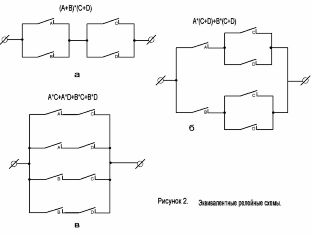
2. Dokažte, že obvody znázorněné na obrázku 3, aab jsou rovnocenné.

3. Zjednodušte obvod zobrazený na obrázku 3;

4. Jaký strukturální vzorec implementuje schéma na obrázku 3, d?

Po tom, co jsme již studovali, bude možné začít řešit problémy, které byly stanoveny na samém začátku prvního článku. Krátce si je vybavujeme.

Prvním úkolem bylo zapnout a vypnout žárovku v místnosti se třemi spínači umístěnými na různých místech: u dveří, u stolu, u postele.

Druhým úkolem je hlasovat o sportovních rozhodčích: ze čtyř rozhodčích musí „FOR“ hlasovat nejméně dva, pokud hlasoval „FOR“ předseda komise.

Třetí úkol byl pouze pro vzdělávací účely. Navrhoval to samé jako v prvním, pouze pro šest spínačů, jako by v místnosti bylo šest stěn. Podobné obvody se právě vyvíjejí pomocí algebry reléových obvodů.

Obecně platí, že pokud chceme vyvinout schéma, které má určité logické vlastnosti, můžeme k tomuto problému přistupovat dvěma různými způsoby. Obvykle lze tyto cesty nazvat „intuitivní“ a „algebraické“.

Některé úkoly jsou lépe vyřešeny na prvním místě, zatímco jiné na druhém. Intuitivní přístup se ukázal být výhodnějším, když je provoz obvodu řízen mnoha přepínači, ale ve vzájemném uspořádání těchto relé existuje určitá symetrie. Uvidíme, že zde intuitivní přístup vede k cíli rychleji, zatímco použití aparátu relační algebry v případě mnoha proměnných může být velmi těžkopádné. Je užitečné seznámit se s oběma možnými přístupy k řešení tohoto problému.

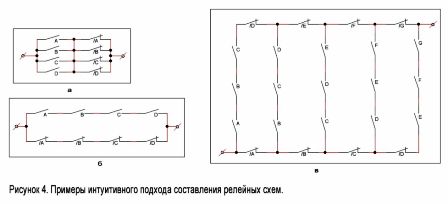
Začněme intuitivním přístupem. Předpokládejme, že jsme potřebovali vybudovat obvod, který byl uzavřen, když fungovaly všechny n řídicí obvody relé.

Řešení tohoto problému nevyžaduje dlouhé uvažování: je zřejmé, že podmínka bude splněna, pokud budou propojeny postupně n normálně rozpojené reléové kontakty.

Podobně je zřejmé, že pro vytvoření obvodu, který se uzavře, když se vypne alespoň jedno z n relé, stačí připojit n normálně otevřených reléových kontaktů paralelně.

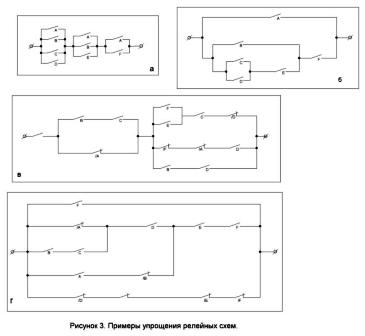
Je snadné si představit obvod, který se uzavře, když se spouští některá, ale ne všechna relé. Takový obvod je znázorněn na obr. 4, a. Obr. Vpravo je schéma, které funguje na principu „vše nebo nic“. Bude sepnout pouze tehdy, když budou všechna relé vypnuta nebo jsou relé odpojena (obrázek 4, 6).

Zvažte nyní složitější příklad. Nechť jsou n kontakty umístěné v určité specifické posloupnosti: A, B, C, D, E, F ... Budeme konstruovat obvod, který se uzavře, když jsou všechny kontakty připojené k sérii uzavřeny, a pouze jsou. Takové schéma pro hodnoty n = 7 a k = 3 je znázorněno na obrázku 4, c. Způsob konstrukce takových schémat pro jakékoli jiné hodnoty n a k je zřejmý z tohoto obrázku.

Pokračujeme konstrukcí obvodů podle daných podmínek jejich práce pomocí reléové algebry.

Stejně jako dříve, provozní podmínky obvodu jsou vždy nejprve nastaveny ústně. Návrhář, především, musí být schopen vyjádřit slovy, co chce. Pokud nemá tak jasnost, nepomůže žádná algebra. Vždy byste měli začít jasným prohlášením o požadavcích, které jsou stanoveny před novým schématem. Stejně jako v každém podnikání je tento úkol pravděpodobně nejobtížnější. Jsou-li podmínky dostatečně jednoduché, můžeme okamžitě napsat výraz strukturního vzorce, který splňuje tyto požadavky.

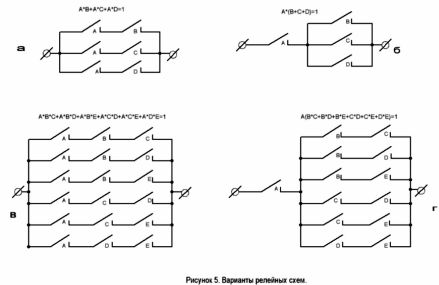
Příklad 1 Předpokládejme, že musíme postavit obvod obsahující 4 kontakty A, B, C a D tak, aby byl obvod sepnut, když je kontakt A sepnut, a jeden z dalších tří kontaktů. V tomto jednoduchém případě bude operace obvodu ve verbálním zápisu vypadat takto: „Okruh by měl vést proud, pokud jsou kontakty A a B uzavřené, nebo kontakty A a C nebo kontakty A a D. Souhlasí, že nyní je velmi snadné sestavit strukturální vzorec. Vypadá to takto:

A * B + A * C + A * D = 1 nebo A * (B + C + D) = 1.

Okruh má dvě možnosti. Jsou zobrazeny na obrázku 5. Druhá možnost nevyžaduje relé se třemi normálně otevřenými kontakty.

Příklad 2 Prvním článkem byl úkol číslo 2 o hlasování sportovních rozhodčích. Podrobněji si přečtěte jeho stav, je podobný jako právě zkoumaný příklad. Jasnější verbální záznam požadavků bude vypadat takto: „Je nutné vytvořit obvod obsahující 5 kontaktů A, B, C, D, E, aby vedl proud a rozsvítil kontrolku displeje, jsou-li tyto kontakty sepnuty:

A a B a C nebo A a B a D nebo A a B a E nebo A a C a D nebo A a C a E nebo A a D a E. Kontakt A je tlačítko předsedy. Pokud není stisknuto, bude každý ze 6 logických produktů 0, tj. Hlasování se neuskutečnilo.

Strukturální vzorec bude následující:

(A * B * C) + (A * B * D) + (A * B * E) + (A * C * D) + (A * C * E) + (A * D * E) = 1,

nebo A * (B * C + B * D + B * E + C * D + C * E + D * E) = 1.

Obě varianty obvodu jsou znázorněny na obr. 5, cad. Toto je řešení problému.

Po přečtení strukturních vzorců je snadné si představit obvod samotného automatu a všechny jeho schopnosti. Je zajímavé, že algebra reléových obvodů poskytuje více informací než samotný obvod. To vám umožní zjistit, kolik a která relé jsou požadována. S jeho pomocí můžete snadno najít nejjednodušší verzi obvodu stroje.

Příklad 3 Po získání zkušeností s přípravou strukturních vzorců se pokusíme vyřešit problém, který začal první článek: je třeba navrhnout spínač, který vám umožní zapnout světlo při vstupu ke dveřím a vypnout jej poté, co jste vyšplhali na požadované podlaží, nebo naopak, zapněte jej při opuštění bytu a vypněte ho, když jdete dolů. Stejná situace nastává na dlouhé chodbě: na jednom konci musí být žárovka rozsvícena a poté, co šla na druhý konec, zhasne. Stručně řečeno, úkol se scvrkává na ovládání jedné žárovky z různých míst pomocí dvou spínačů.

Pro řešení problému zvolíme následující postup: Nejprve si jasně formulujeme provozní podmínky spínačů, pak je zapíšeme do vzorce a na základě toho nakreslíme elektrický obvod.

Aby žárovka shořela (1), je nutné, aby byla splněna jedna ze dvou podmínek:

1. Zapněte spínač na spodní straně (A) a vypněte nahoře (/ B). Zadejte verandu.

2. Zapněte spínač nahoře (B) a vypněte dno (/ A).

S použitím přijaté notace je strukturní vzorec psán následovně:

A * (/ B) + (/ A) * B = 1

Schéma zapojení spínače je znázorněno na obrázku 6. V současné době jsou takové spínače komerčně dostupné, jedná se o tzv přepínače průchodky. Proto se zde uvažuje pouze o koncepcích obecných principů jejich práce.

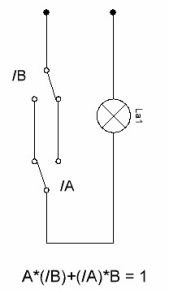
Obrázek 6

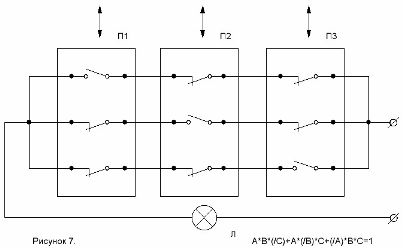
V úkolu č. 1 na začátku prvního článku jsme hovořili o schématu, které vám umožňuje zapnout a vypnout světlo v místnosti pomocí některého ze tří přepínačů. Stejným způsobem jako v případě dvou přepínačů získáme strukturní vzorec:

A * B * (/ C) + A * (/ B) + (/ A) * B * C = 1.

Schéma sestavené tímto vzorcem je znázorněno na obrázku 7.

Obrázek 7

Na začátku prvního článku byl navržen jednoduchý vzdělávací úkol č. 2: jako by v místnosti bylo šest stěn a každá z nich měla vypínač. Logika obvodu je přesně stejná jako u tří spínačů. Označme je písmeny A, B, C, D, E, F. Připomeňme, že notace (/ A), (/ B) atd., Nejedná se o znak dělení, ale o logickou negaci. Častěji označují podtržení znaků a dokonce i celé výrazy nahoře. V některých schématech je toto podtržítko jednoduše nahrazeno znaménkem mínus. Strukturální vzorec pro šest přepínačů je tedy:

(/ A) * B * C * D * E * F + A * (/ B) * C * D * E * F + A * B * (/ C) * D * E * F + A * B * C *

(/ D) * E * F + A * B * C * D * (/ E) * F + A * B * C * D * E * (/ F) = 1.

Čtenáři jsou vyzváni, aby vypracovali kompletní elektrický obvod, který implementuje tento strukturní vzorec, aby získali praktické dovednosti při navrhování obvodů. Trocha nápověda: pro obvod budete potřebovat šest relé, z nichž každé má jeden normálně otevřený kontakt a pět normálně uzavřených. Taková složitá relé mohou být v případě potřeby sestavena z několika jednodušších spojením jejich cívek paralelně.

Tím se uzavírá příběh booleovské algebry a algebry reléových obvodů.

Pokračování článku: Logické čipy

Boris Aladyshkin