Booleovská algebra. Část 1. Trocha historie

Ve škole jsme všichni studovali algebru, ale nemluvili o booleovské algebře. Jaký je rozdíl mezi booleovskou algebrou a školní algebrou, historie jejího vzhledu, problémy a aplikace, jsou popsány v tomto článku.

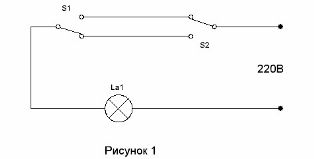
Okruh, který umožňuje dvěma spínačům zapnout světlo v chodbě u vstupu do chodby a vypnout jej při vstupu do místnosti, je znám již velmi dlouhou dobu (viz. Ovládací obvod osvětlení koridoru) Je to znázorněno na obrázku 1.

Úkol číslo 1. Složitější. Vytvořte schéma, které vám umožní zapnout a vypnout světlo ve vaší místnosti pomocí 3 různých přepínačů. Spínače jsou umístěny u vstupu do místnosti, nad postelí a u stolu.

Úkol číslo 2.

Ve sportovní komisi, jako je tovární komise, se shromáždilo 5 rozhodčích.

Každý z nich musí hlasovat pro jiná rozhodnutí. Rozhodnutí je přijato většinou hlasů, avšak pouze za podmínky, že za to hlasuje předseda výboru.

Rozhodčí hlasují stisknutím tlačítka, které uzavírá spínač umístěný pod stolem, na kterém sedí. Uzavřením přepínače hlasují pro, čímž se odpojí zápory. Nakreslete jednoduchý diagram, který vám umožní automaticky zobrazit výsledky hlasování. V nejjednodušším případě, jednoduše pomocí žárovky - svítí - bylo učiněno rozhodnutí, nesvítilo - ne.

Úkol číslo 3. V praxi je to nepravděpodobné, ale jako složitý vzdělávací úkol je docela vhodný.

Ve velké šestihranné místnosti je na každou stěnu nainstalován jeden spínač. Postavte obvod tak, abyste kdykoli mohli zapnout nebo vypnout světlo v místnosti otočením jednoho (libovolného) spínače.

Poté, co neúspěšně sedíte nad úkoly na tři až čtyři dny, dočasně je odložte. A zaneprázdněn Booleovská algebra. Je to booleovská algebra nebo, jak se také říká, Booleovská algebra, algebra reléového obvodu, pomůže vám vyřešit vaše problémy.

Co je booleovská algebra?

Kupodivu, navzdory skutečnosti, že pět let studují algebra ve škole, mnoho studentů a později dospělých nebude schopno odpovědět na otázku, co je algebra? Algebra je věda, která studuje soubory některých prvků a akce na nich.

Ve školním kurzu algebry jsou takové prvky čísla. Čísla nelze označovat čísly, nýbrž písmeny, to všichni znají. V prvních lekcích algebry to vždy komplikovalo mnoho studentů. Vzpomeňte si, jak těžké bylo zpočátku zvyknout si skládat písmena místo čísel, řešit rovnice, které neřekly nic.

Pravděpodobně si každý z nás položil otázku: „Proč musíme místo čísel zadávat písmena a je to vůbec nutné?“ A teprve později jste viděli, jaké výhody algebra dává při řešení problémů ve srovnání s aritmetikou.

Algebra se používá v mnoha přesných vědách. Toto je fyzika, mechanika, sopromat, elektřina. Ohmův zákon není nic víc než algebraická rovnice: stačí nahradit jejich číselné hodnoty místo písmen, abychom zjistili, jaký proud bude proudit v zátěži nebo jaký odpor má část obvodu.

Seznámili jste se tedy s algebrou čísel nebo s elementární algebrou. Hlavním a téměř jedinečným úkolem je získat odpověď na otázku: „Co se rovná X? Kolik? “

Na střední škole studují začátky vektorové algebry. Tato algebra se zásadně liší od základní algebry. Má odlišnou povahu studovaného souboru a dalších pravidel jednání. Řešením vektorové rovnice dostaneme v odpovědi vektor, který není obyčejným číslem, které odpovídá na otázku „Kolik?“

Vzorce vektorové algebry se v mnoha ohledech liší od vzorců elementární algebry. Například v elementární algebře a ve vektorové algebře je operace sčítání. Provádí se však úplně jinak.Přidávání čísel není vůbec stejné jako přidávání vektorů.

Existují i ​​další algebry: lineární algebra, algebra struktur, algebra prstenů, algebra logiky nebo, co je stejné, booleovská algebra. Pravděpodobně jste ve školních hodinách neslyšeli jméno. George Boole - ale každý zná jméno své talentované dcery Ethel Voinich (1864 - 1960). Napsala román Gadfly, který hovoří o boji za práva italských karbonářů.

George Bull se narodil v Anglii 2. listopadu 1815. Celý život pracoval jako učitel matematiky a fyziky ve škole. Z pamětí jeho studentů je známo, jak velký význam přikládal Bul rozvoju tvůrčích schopností studentů. Při prezentaci nového materiálu se snažil zajistit, aby jeho studenti sami „znovuobjevili“ určité vzorce a zákony.

Učitel vyprávěl studentům o obtížích, kterým vědci nevyhnutelně čelili při hledání pravdy, učitel rád opakoval jednu východní moudrost: ani perský trůn nemůže člověku přinést tolik potěšení jako nejmenší vědecký objev. Buhl nikdy neztratil naději, že jednoho dne jeho studenti udělají skutečný objev.

Rozsah vědeckých zájmů Buhl byl velmi široký: stejně se zajímal o matematiku a logiku - vědu o zákonech a formách myšlení. V té době byla logika považována za humanitní vědu a mnozí, kteří věděli, že George Boole byl ohromen tím, jak přesné metody poznávání vlastní matematice a čistě popisné metody logiky mohou existovat u jedné osoby.

Ale vědec chtěl, aby věda o zákonech a formách myšlení byla stejně přísná jako kterákoli z přírodních věd, řekněme matematika a fyzika. Za tímto účelem začala Boule označovat ne čísla jako písmena, jak se to děje v obyčejné algebře, ale prohlášení, a ukázala, že takové rovnice, velmi podobné algebraickým, mohou řešit otázky o pravdě a nepravdivosti výroků člověka. Booleovská algebra tedy vznikla.

Ale dlouho předtím, než George Buhl, německý matematik a filozof Gottfried Leibniz (1646-1716) poprvé vyjádřil myšlenku vytvoření vědy, která by označovala všechny koncepty obyčejné hovorové řeči se symboly a vytvořila nějakou novou algebru pro kombinování těchto symbolů.

Po vytvoření takové vědy se podle Leibnize vědci a filozofové přestanou hádat a křičet na sebe, hledat pravdu, ale zvednou tužku a klidně řeknou: „Pojďme spočítat!“

Dnes se algebra logiky stala důležitou součástí matematiky. Jedním z jeho úkolů je řešit všechny druhy rovnic, jejichž číselné poměry jsou nahrazeny abecedními. Každý z vás si pravděpodobně celý život pamatoval, jak řešit rovnice druhého a třetího stupně koeficienty písmen. Boole tedy ve své nové algebře použil všechny tyto vzorce a pravidla.

Co je nového v Booleovské algebře je to, že prvky množiny, které jsou v ní studovány, nejsou čísla, ale příkazy. Pokud je při řešení obyčejných algebraických rovnic určeno, jaké číslo je neznámé X stejné, školní algebra hledá odpověď na otázku: „Kolik?“

Algebra logiky hledá odpověď na otázku: „Je toto nebo toto tvrzení označeno písmenem X pravdivé?“

Význam a obsah prohlášení zde nehrají žádnou roli. Každé tvrzení může být pouze pravdivé nebo nepravdivé. Nemůže to být napůl pravda a napůl nepravda. Jako příklad si můžeme vzpomenout na to, že hodíme hodně mincí.

Jsou zde uvažovány pouze dva stavy mincí - hlavy nebo ocasy. Po dohodě stran je orel ANO a ocasy NE. V teorii pravděpodobnosti nejsou brány v úvahu žádné další mezilehlé body, i když jsou možné. Převrácená mince může spadnout na okraj, převrátit podlahu k nohám židle nebo stolu a zůstat ve vzpřímené poloze nebo dokonce spadnout do široké mezery v podlaze. (Analogicky s elektrickými obvody lze poslední dvě situace považovat za poruchu ve formě spáleného kontaktu).Ale v té době nebyla bohužel používána booleovská algebra.

Claude Shannon znovu „objevil“ Buhlovu algebru. V roce 1938, ještě jako student technologického institutu v Massachusetts a Americe, mladý Claude dokázal, že booleovská algebra je zcela vhodná pro analýzu a syntézu reléových a spínacích obvodů.

S pomocí booleovské algebry je velmi snadné vyrobit elektrický obvod reléového stroje.Ukazuje se, že potřebujete přesně vědět, co by měl stroj dělat, to znamená, že pro jeho provoz musíte mít algoritmus. Základ byl položen pro teorii digitálních strojů fungujících na principu ANO nebo NE.

Taková, v krátkosti, je historie booleovské algebry. V následujících článcích se budeme zabývat jeho základními zákony, příklady kontaktních obvodů implementujících tyto zákony. Zvažte řešení těch úkolů, které byly zadány na začátku článku.

Pokračování článku: Booleovská algebra. Část 2. Základní zákony a funkce

Boris Aladyshkin