Booleovská algebra. Část 2. Základní zákony a funkce

Pokračování příběhu o booleovské algebře, konvence, pravidla, operace. Přechod k základům kontaktních obvodů.

V první článek George Bull byl popisován jako tvůrce algebry logiky. Druhý článek popisuje základní operace booleovské algebry a metody pro zjednodušení booleovských výrazů. Booleovská algebra tedy používá tvrzení jako argumenty, nikoli jejich význam, ale pravdivost nebo nepravdivost tvrzení.

Formulář pro psaní výrazů v booleovské algebře.

Pokud je výrok pravdivý, pak se píše takto: A = 1, je-li nepravdivý, pak A = 0 (konec konců není pravda, že brambor je ovoce). Pro každý příkaz je A buď true (A = 1) nebo false (A = 0). Zde nemůže být žádný prostřed. Už jsme o tom mluvili.

Pokud spojíte dva jednoduché příkazy s unií A, získáte komplexní příkaz, který se nazývá logický produkt. Vezměme si dvě jednoduchá slova: „Tři jsou více než dvě“ označíme písmenem A, „Tři méně než pět“ - písmenem B.

Proto je složité tvrzení „Tři je více než dva A méně než pět“ logické (v tomto případě velké písmeno A říká, že se jedná o logickou operaci „A“ a později v textu „NEBO“ a „NE“). a B. Označuje se takto: A ^ B nebo A * B.

Logické násobení (operace „AND“).

V elementární algebře A * A = A2. Ale v Buhlově algebře A * A = A2 = A, A * A = A, protože znaménko násobení (*) nyní znamená ... A ... ve smyslu A ... A. Všechny naše zkušenosti potvrzují, že A&A je stejná jako v případě A. S tím nelze nesouhlasit. Pravda prohlášení se nemění, pokud je faktorem několikrát opakována.

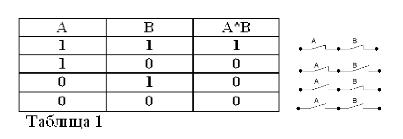
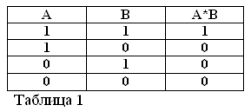
Produkt dvou výroků je tedy považován za pravdivý (roven 1) a pouze tehdy, jsou-li oba faktory pravdivé, a nepravdivý (roven 0), pokud je alespoň jeden z faktorů nepravdivý. Souhlasíte s tím, že tato pravidla nejsou v rozporu se zdravým rozumem a navíc plně dodržují pravidla elementární algebry:

1*1 = 1, 1*0 = 0 = 0*1 = 0, 0*0 = 0.

První rovnost zní následovně: pokud jsou obě A a B pravdivé, pak je produkt A * B pravdivý. V Buhl algebře nahrazuje znak násobení (*) unii I.

Logické produkty nemusí obsahovat dva, ale větší počet výroků - faktorů. A v tomto případě je produkt pravdivý pouze tehdy, jsou-li současně všechny výrokové faktory pravdivé.

Logické sčítání (NEBO operace)

Pokud jsou dvě prohlášení spojena odborem NEBO. ta vytvořená složená věta se nazývá logická suma.

Vezměme si příklad logického součtu. Řekl A: „Dnes půjdu do kina.“

Prohlášení B: „Dnes půjdu na diskotéku.“ Přidáme obě prohlášení a dostaneme: „Dnes půjdu k filmům NEBO na diskotéku.“

Toto složité tvrzení je označeno takto: A + B = C nebo (A V B) = C.

C jsme označili jako komplexní výpis logické částky.

V uvažovaném příkladu nelze unie NEBO použít v exkluzivním smyslu. Ve stejný den se můžete dostat do kina a na diskotéku. A tady je rčení:

„Předsedou zahradnického partnerství bude Petrov nebo Ivanov,“ není logická částka, protože předsedou bude pouze jedna osoba a druhá amatérský obyčejný zahradník.

Znaménko V pro logický součet je zvoleno proto, že se jedná o počáteční písmeno latinského slova „vel“, což znamená „nebo“, na rozdíl od latinského slova „aut>, což znamená„ a “. Nyní by mělo být každému jasné, proč je logický produkt označen znakem ^.

V elementární algebře existuje pravidlo A + A = 2A. Toto pravidlo je pravda, bez ohledu na to, jaké číslo je reprezentováno písmenem A. V booleovské algebře tomu odpovídá pravidlo A + A = A. Naše celá životní zkušenost říká, že říkat A NEBO nebo oba A je jen další a delší způsob, jak říci jen A.

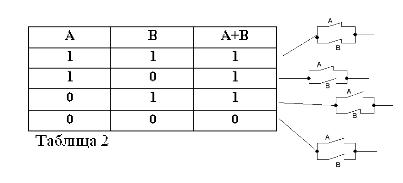
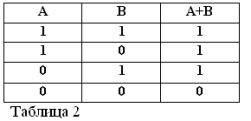
Stejně jako jakékoli složené tvrzení může být součet obou tvrzení A a B pravdivý nebo nepravdivý. Součet je považován za pravdivý, tj. Rovný jednotě, je-li pravdivá alespoň jedna z podmínek:

A + B = 1, pokud OR A = 1 nebo B = 1, což je v souladu s konvenční aritmetikou:

1+0 = 0+1 = 1.

Jsou-li oba sumované příkazy pravdivé, je součet považován za pravdivý, a proto v booleovské algebře máme: (1) + (1) = 1.

Konzoly jsou zde nastaveny tak, aby zdůrazňovaly podmíněnost, význam tohoto sčítání a ne aritmetiku.

Součet dvou příkazů je považován za nepravdivý a roven nule, pokud, ale pouze pokud jsou oba termíny nepravdivé. Odtud:

0 + 0=0.

Součet obou výroků A + B je tedy považován za pravdivý, pokud je pravdivý, OR A, OR B, NEBO oba termíny dohromady. Slovo OR je tedy označeno +.

Vzhledem k tomu, že výroky A a B mohou být pouze pravdivé nebo nepravdivé, a proto mají míru pravdy 1 nebo 0, lze výsledky zvažovaných operací AND a OR shrnout v tabulkách 1 a 2.

Třetí operace, kterou Buhlova algebra často používá, je operace negace - NE. Připomínáme, že elementární algebra používá operace ADD, D Odečíst, Násobit, Rozdělit a některé další.

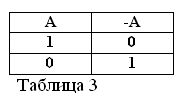
U každého výroku A existuje jeho negace NOT A, kterou označíme symbolem / A. To by nemělo být na pochybách.

Uvádíme příklady: „Půjdeme do lesa“ A, „Půjdeme do lesa“ / A.

Pokud je výrok A pravdivý, tj. A = 1, pak jeho negace / A musí být nepravdivá / A = 0. A naopak, pokud je jakýkoli výrok nepravdivý, pak je jeho negace pravdivá. Například: „Kůň nejí seno“ / A = 0, „Kůň nejí seno“ (A = 1). To lze vyjádřit v tabulce 3.

Stanovení významu působení negace a za předpokladu, že z obou výroků A a / A je vždy jedna pravda, následují dva nové vzorce booleovské algebry:

A + (/ A) = 1 a A * (/ A) = 0.

Existují také jiné vzorce, které zjednodušují logické zpracování příkazů. Například 1 + A = 1, protože podle definice sčítání je v případě, kdy je jeden člen roven jednotě, součet vždy roven jednotě. Získaný výsledek nezávisí na tom, zda A = 0 nebo A = 1.

Každá ze tří zkoumaných logických operací (AND, OR, NOT) má určité vlastnosti, které jsou blízké pravidlům elementární algebry. Pokud jsou všechny formulovány, získáme 25 pravidel booleovské algebry. Jsou dostačující, aby vyřešili téměř jakýkoli logický problém. Bez těchto pravidel se stává docela obtížné řešit logické problémy kvůli jejich zjevné složitosti. Snažit se najít správnou odpověď bez použití pravidel znamená nahradit je vynalézavostí a obecným zdůvodněním. Pravidla velmi usnadňují tuto práci a šetří čas.

V rámci článku není možné zvážit všech těchto 25 pravidel, ale ti, kdo si to přejí, je vždy najdou v příslušné literatuře.

Jak již bylo zmíněno v prvním článku v roce 1938, mladý americký vědec Claude Shannon ve svém článku „Symbolická analýza reléových a spínacích obvodů“ poprvé používá booleovskou algebru k problémům s technologií přenosu. Shannonův objev spočíval v tom, že si uvědomil, že metoda navrhování reléových strojů a elektronických počítačů je ve skutečnosti oborem matematické logiky.

Často se to stává. Po mnoho let vědec pracuje na problému, který se jeho krajanům zdá být zcela zbytečný - jen zábava. Ale uplynou desetiletí a někdy i staletí a teorie, kterou nikdo nepotřebuje, nezískává pouze právo na existenci, ale bez ní se další pokrok stane nemyslitelným.

Co pomohlo Shannonovi podruhé „objevit“ booleovskou algebru? Pouzdro? Nic takového.

Láska k reléovým strojům, postaveným na konvenčních spínačích a relé, pomohla mladému vědci spojit zapomenutou teorii s úkoly automatických telefonních ústředen, na kterých v té době pracoval. Později Shannon představil stejnou myšlenku „ano nebo ne“ do diskrétních zpráv a položil základy celé části kybernetiky - informační teorii.

Buhlova algebra byla velmi vhodná pro analýzu a syntézu reléových obvodů. Stačilo přijmout jako pravdivé tvrzení: „V obvodu je signál“ a jako falešný - „V obvodu není signál“, jak se objevila nová algebra - signální algebra, algebra reléového obvodu.

Nová algebra platí pouze pro posouzení reléových a spínacích obvodů. Ve skutečnosti je pouze u takových schémat splněna podmínka „existuje signál“ a „žádný signál“. Tam, kde se signál neustále mění a získává libovolně velké množství přechodných podmínek (takový signál se nazývá analogový), není algebra relé použitelná. To musí být vždy zapamatováno. Ale jen většina elektronických počítačů a kybernetických strojů používá diskrétní princip zpracování signálu, který je založen na prvcích „ano - ne“.

Výraz „kontakt uzavřen“ byl Shannonem přijat jako pravdivý (1) a „kontakt otevřen“ jako nepravdivý (0). Zbytek „algebry“, včetně operací AND, OR, NOT a 25 pravidel, si Shannon půjčil od Boole.

Algebra reléového obvodu se ukázala být jednodušší než logická algebra, protože se zabývá pouze prvky typu ano-ne. Nová algebra je navíc vizuálnější.

Prvky v této algebře jsou kontakty, které označíme písmeny A, B, C ... Kontakt je sepnut - A, kontakt je otevřen - / A (písmeno s pomlčkou).

Jak vidíte, zápis je zcela převzat z booleovské algebry. Otevřený kontakt je negace uzavřeného kontaktu. Stejný kontakt nelze zavřít ani otevřít.

Souhlasíme, že pokud jsou v jakémkoli obvodu dva kontakty označeny stejným písmenem, znamená to, že vždy berou stejné hodnoty.

V kterémkoli daném okamžiku jsou oba otevřeni současně nebo oba uzavřeni. Nejjednodušší způsob, jak si je představit, jsou mechanicky spojeny, aby se oba otevřely nebo zavřely současně.

Pokud je kontakt v nějakém řetězci negací jiného kontaktu, jejich význam je vždy opačný. Například kontakty C a / C nemohou být nikdy otevřeny nebo současně uzavřeny. A v diagramu mohou být znázorněny mechanicky spojené: pokud se jeden z nich otevře, druhý se uzavře.

Začínáme seznámení s relační algebrou analýzou nejjednodušších obvodů odpovídajících operacím AND, OR a NOT.

Produkt dvou kontaktů (operace AND) je obvod získaný v důsledku jejich sériového spojení: je uzavřen (rovná 1), pouze když jsou oba kontakty sepnuty (rovnající se 1).

Součet dvou kontaktů (operace OR) bude tvořen obvodem, když jsou spojeny paralelně: je uzavřen (rovná 1), když je uzavřen alespoň jeden z kontaktů tvořících obvod (roven 1).

Opakem tohoto kontaktu (operace NOT) je kontakt rovný 0 (otevřený), pokud je tento kontakt 1 (sepnutý), a naopak.

Stejně jako v booleovské algebře, pokud jsou kontakty označeny písmeny A a B, označíme součin dvou kontaktů A * B, součet A + B a kontakt opačný A, podle / A. Výše uvedené je vysvětleno na obrázcích 1, 2 a 3.

Platnost tabulek odpovídajících operacím AND, OR a NOT. teď by nikdo neměl pochybovat.

Pojďme se zabývat dvěma příklady: 1 * 0 = 0 a 1 + 0 = 1.

Z obrázku je vidět, že trvale uzavřený kontakt zapojený do série s trvale otevřeným kontaktem je ekvivalentem trvale otevřenému kontaktu (1 * 0 = 0). Trvale uzavřený kontakt spojený paralelně s trvale otevřeným kontaktem je ekvivalentem trvale uzavřenému kontaktu.

Po seznámení s aritmetikou kontaktních obvodů můžete popsat jakýkoli reléový obvod pomocí vzorce pomocí přijatých konvencí. V kybernetice se takové vzorce nazývají strukturální.

Pokud je strukturní vzorec některého reléového obvodu 1, pak ním může procházet signál - obvod je uzavřen. Naopak, pokud je strukturní vzorec obvodu 0, signál tímto signálem neprochází - obvod je přerušen.Závěr: dva reléové obvody jsou si navzájem rovnocenné, když jsou jejich strukturní vzorce stejné.

V pokračování článku se budeme zabývat příklady kontaktních obvodů, typických kontaktních obvodů a jejich ekvivalentů, jakož i vypracováním diagramů pomocí strukturních vzorců. Uvažujeme také o hlavních logických obvodech, které vykonávají funkce booleovské algebry.

Pokračování článku: Booleovská algebra. Část 3. Kontaktní schémata

Boris Aladyshkin