ตัวเก็บประจุในวงจรอิเล็กทรอนิกส์

ในบทความก่อนหน้านี้เราได้พูดคุยสั้น ๆ เกี่ยวกับการทำงานของตัวเก็บประจุในวงจร AC อย่างไรและทำไมตัวเก็บประจุผ่านกระแส AC (ดู - ตัวเก็บประจุ AC) ในกรณีนี้ตัวเก็บประจุจะไม่ร้อนขึ้นพลังงานไม่ได้ถูกจัดสรรให้กับพวกเขา: ในครึ่งคลื่นหนึ่งของไซน์ไซด์ประจุตัวเก็บประจุและอีกตัวหนึ่งจะปล่อยประจุตามธรรมชาติในขณะที่ถ่ายโอนพลังงานที่เก็บไว้กลับไปยังแหล่งกำเนิดปัจจุบัน

วิธีการส่งผ่านกระแสไฟฟ้านี้ช่วยให้คุณสามารถเรียกความต้านทานอิสระของตัวเก็บประจุได้และนั่นคือสาเหตุที่ตัวเก็บประจุที่เชื่อมต่อกับเต้าเสียบไม่ได้หมุนตัวนับ และทั้งหมดนี้เป็นเพราะกระแสในตัวเก็บประจุอยู่ก่อน 1/4 ของเวลาที่แรงดันใช้

แต่ระยะนี้ล่วงหน้าทำให้ไม่เพียง แต่ "หลอก" ตัวนับเท่านั้น แต่ยังทำให้สามารถสร้างวงจรต่าง ๆ ได้เช่นเครื่องกำเนิดสัญญาณไซน์และสัญญาณรูปสี่เหลี่ยมความล่าช้าของเวลาและตัวกรองความถี่ต่างๆ

ในกระบวนการของเรื่องนี้บางครั้งเราจะต้องนึกถึงสิ่งที่ได้พูดไปแล้วก่อนหน้าดังนั้นเพื่อพูดเพื่อสรุป วิธีนี้จะช่วยไม่ให้ย้อนกลับไปยังบทความก่อนหน้าเพื่อเรียกคืนสูตรอย่างง่าย ๆ หรือเพียงแค่ "มันคืออะไร"

การเชื่อมต่อแบบอนุกรมและอนุกรมของตัวเก็บประจุ

ด้วยการเชื่อมต่อตัวเก็บประจุแบบขนานความจุทั้งหมดเป็นเพียงผลรวมทางคณิตศาสตร์ของความจุ โดยธรรมชาติเมื่อรวมเข้าด้วยกันนี้ความจุทั้งหมดจะมากกว่าความจุของตัวเก็บประจุที่ใหญ่ที่สุด Ctotal = C1 + C2 + C3 + ... + Cn

ในกรณีของการเชื่อมต่อแบบอนุกรมความจุรวมจะน้อยกว่าความจุที่เล็กที่สุด

1 / Ctotal = 1 / C1 + 1 / C2 + 1 / C3 + ... + 1 / Cn

เมื่อเชื่อมต่อตัวเก็บประจุที่เหมือนกันสองชุดเป็นชุดความจุรวมจะเท่ากับครึ่งหนึ่งของความจุหนึ่ง: ตัวอย่างเช่นเมื่อเชื่อมต่อตัวเก็บประจุสองตัวที่ 1 µF แต่ละตัวเก็บประจุทั้งหมดจะเป็น 0.5 µF

ความจุ Xc

ที่นี่ทุกอย่างเช่นเดียวกับเมื่อเชื่อมต่อตัวต้านทานเป็นสิ่งที่ตรงกันข้ามอย่างแน่นอน: การเชื่อมต่อแบบอนุกรมจะลดความจุทั้งหมดและขนานหนึ่งจะเพิ่มขึ้น ไม่ควรลืมกรณีนี้เมื่อเชื่อมต่อตัวเก็บประจุเนื่องจากความจุที่เพิ่มขึ้นนำไปสู่การลดลงของความจุ Xc

Xc = 1/2 * π * f * C

จากมุมมองของคณิตศาสตร์นี่ค่อนข้างเป็นธรรมชาติเพราะความสามารถ C อยู่ในส่วนของเศษส่วน โดยวิธีการที่ความถี่ f อยู่ในสถานที่เดียวกันดังนั้นการเพิ่มความถี่ก็นำไปสู่การลดลงของความจุ Xc ความหมายทางกายภาพของสิ่งนี้คือผ่านตัวเก็บประจุเดียวกันมันจะดีกว่าไม่ จำกัด มากขึ้นและผ่านความถี่สูง สิ่งนี้จะถูกกล่าวถึงในภายหลังเมื่อพูดถึงตัวกรอง low-pass และ high-pass

หากเราใช้ตัวเก็บประจุที่มีความจุ 1 μFดังนั้นสำหรับความถี่ 60 Hz Xc ของมันจะเป็น 2653 โอห์มและสำหรับความถี่ 400 Hz ตัวเก็บประจุเดียวกันมี Xc เพียง 398 โอห์ม ผู้ที่ต้องการสามารถตรวจสอบผลลัพธ์เหล่านี้ได้โดยสูตรการแทนที่π = 3.14 ความถี่เป็นเฮิร์ตซ์และความจุในฟาราด จากนั้นผลลัพธ์จะเป็นโอห์ม ทุกอย่างจะต้องสอดคล้องกับระบบ SI!

แต่ตัวเก็บประจุจะใช้ไม่เพียง แต่เป็นตัวต้านทานการทำให้หมาด ๆ ฟรีหรือในตัวกรอง rectifier โดยไม่ต้องมีส่วนร่วมวงจรสำหรับเครื่องกำเนิดไฟฟ้าความถี่ต่ำและสูงตัวแปลงรูปคลื่นต่าง ๆ วงจรแยกและรวมวงจร เครื่องขยายเสียง และแผนการอื่น ๆ

ถัดไปจะพิจารณาสัญญาณไฟฟ้าต่างๆที่ตัวเก็บประจุทำงานด้วย ประการแรกสิ่งเหล่านี้เป็นสัญญาณที่เหมาะสำหรับการสังเกตด้วย สโคป.

ระยะเวลาและความถี่ของการแกว่ง

การแกว่งเป็นระยะจึงเรียกว่าคาบซึ่งโดยไม่มีการหยุดยั้งจะทำซ้ำรูปแบบเดียวกันตัวอย่างเช่นการสั่นแบบไซน์หนึ่งครั้ง ระยะเวลาของการแกว่งเต็มนี้เรียกได้อย่างแม่นยำว่าช่วงเวลา T และวัดเป็นวินาทีวินาทีมิลลิวินาทีไมโครวินาทีอุปกรณ์อิเล็กทรอนิกส์ที่ทันสมัยแม้จะเกี่ยวข้องกับนาโนวินาที (หนึ่งในพันล้านต่อวินาที)

จำนวนระยะเวลาต่อวินาทีเรียกว่าความถี่ (ความถี่) ของการสั่น f และแสดงเป็นเฮิรตซ์ 1Hz คือความถี่ที่การแกว่งหนึ่งครั้งหนึ่งรอบระยะเวลาเต็มดำเนินการใน 1 วินาที อัตราส่วนของรอบระยะเวลาและความถี่แสดงโดยสูตรอย่างง่าย T = 1 / f

ดังนั้นการรู้ระยะเวลาการแกว่งจึงง่ายมากในการคำนวณความถี่ f = 1 / T

นี่คือวิธีคำนวณความถี่เมื่อวัดด้วยออสซิลโลสโคป: จำนวนเซลล์ในช่วงเวลาถูกคำนวณคูณด้วยระยะเวลาของเซลล์เดียวและได้รับช่วงเวลาเช่นในหน่วยไมโครวินาที และเพื่อหาความถี่พวกเขาใช้สูตรสุดท้าย

สามัญ ออสซิลโลสโคปอิเล็กทรอนิกส์ ช่วยให้คุณสังเกตสัญญาณเป็นระยะ ๆ ที่สามารถซิงโครไนซ์กับความถี่การกวาดเพื่อให้ได้ภาพนิ่งที่เหมาะสำหรับการวิจัย หากคุณส่งสัญญาณไปยังโปรแกรมเพลงไปยังอินพุตของออสซิลโลสโคปคุณจะไม่สามารถหยุดภาพเพื่อทำสิ่งใด เพื่อสังเกตสัญญาณดังกล่าวจะใช้ออสซิลโลสโคปจัดเก็บข้อมูล

เมื่อมีการวัดระยะเวลาเป็นมิลลิวินาทีความถี่จะได้รับเป็นกิโลเฮิร์ตซ์สำหรับช่วงเวลาที่วัดเป็นไมโครวินาทีความถี่นั้นแสดงเป็นเมกะเฮิร์ตซ์แล้ว นี่คือถ้าคุณไม่ปฏิบัติตามข้อกำหนดของระบบ SI: ระยะเวลาเป็นวินาที, ความถี่เป็นเฮิรตซ์

การสั่นสะเทือนแบบไม่มีไซน์

ดังที่ได้กล่าวไว้ก่อนหน้านี้คลื่นซายน์เป็นคลื่นที่พบได้บ่อยที่สุดและเหมาะสมสำหรับการศึกษาและการใช้ประโยชน์ของเส้นโค้งเป็นระยะ ในสภาวะอุตสาหกรรมมันได้มาจากการใช้เครื่องกำเนิดไฟฟ้าเช่นในโรงไฟฟ้าพลังน้ำ ในอุปกรณ์อิเล็กทรอนิกส์จะใช้การสั่นของรูปร่างที่หลากหลายที่สุด

โดยพื้นฐานแล้วรูปแบบเหล่านี้มี 3 รูปแบบคือไซน์ไซดอลสี่เหลี่ยมและสามเหลี่ยมดังแสดงในรูปที่ 1 ทั้งกระแสและแรงดันไฟฟ้าสามารถมีรูปร่างดังกล่าวได้ดังนั้นรูปจะแสดงเฉพาะแกนเวลาเท่านั้น

ความผันผวนดังกล่าวถูกสร้างขึ้นโดยวงจรอิเล็กทรอนิกส์พิเศษ สัญญาณรูปสี่เหลี่ยมผืนผ้าและรูปสามเหลี่ยมมักจะถูกเรียกว่าพัลซิ่ง อย่างไรก็ตามมีวงจรอิเล็กทรอนิกส์จำนวนมากที่ทำหน้าที่แปลงสัญญาณตัวอย่างเช่นรูปสี่เหลี่ยมผืนผ้าสี่เหลี่ยมผืนผ้าสามารถสร้างจากไซน์ไซด์

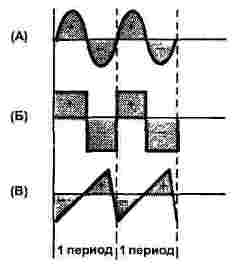
รูปที่ 1

สำหรับสัญญาณทั้งสามรูปแสดงสองจุดสัญญาณทั้งหมดมีความถี่เท่ากัน

สเปกตรัมของสัญญาณที่ไม่ใช่ไซน์

สัญญาณไฟฟ้าใด ๆ สามารถแทนการวัดแอมพลิจูดได้ในบางช่วงเวลา ความถี่ของตัวอย่างเหล่านี้เรียกว่าความถี่สุ่มตัวอย่างและอย่างน้อยสองเท่าสูงกว่าความถี่สูงสุดของสัญญาณที่วัดได้ จากตัวอย่างเหล่านี้คุณสามารถกู้คืนสัญญาณดั้งเดิมได้ ตัวอย่างนี้ใช้วิธีการนี้ในการบันทึกเสียงแบบดิจิทัล วิธีนี้เรียกว่าการวิเคราะห์เวลา

อีกวิธีหนึ่งสันนิษฐานว่าสัญญาณใด ๆ แม้แต่รูปสี่เหลี่ยมผืนผ้าสามารถแสดงเป็นผลรวมเชิงพีชคณิตของไซนัสด้วยความถี่และเฟสที่ต่างกัน วิธีนี้เรียกว่าการวิเคราะห์ความถี่ แต่สิ่งที่ถูกกล่าวว่า“ ด้วยความถี่ที่แตกต่างกัน” นั้นไม่เป็นความจริงอย่างสิ้นเชิง: ไซนัสด์ที่เป็นส่วนประกอบนั้นเรียกว่าฮาร์โมนิกและความถี่ของพวกเขาจะปฏิบัติตามกฎหมายบางอย่าง

คลื่นไซน์ที่มีความถี่เท่ากับความถี่ของคลื่นสี่เหลี่ยมเรียกว่าพื้นฐานหรือฮาร์โมนิแรก แม้แต่ฮาร์โมนิกก็สามารถหาได้จากการคูณความถี่พื้นฐานด้วยเลขคู่และฮาร์มอนิกส์ที่แปลกตามลำดับโดยคี่

ดังนั้นหากฮาร์โมนิกแรกมีความถี่ 1,000 เฮิร์ตซ์ดังนั้นอันที่สองคือ 2000 เฮิร์ตซ์ส่วนที่สี่คือ 4,000 เฮิร์ต เสียงประสานที่แปลกจะมีความถี่ 3000Hz, 5000Hz ยิ่งไปกว่านั้นฮาร์มอนิกแต่ละตัวมีขนาดเล็กกว่าแอมพลิจูดหลัก: ยิ่งฮาร์มอนิกมีความสูง

ในดนตรีฮาร์มอนิกส์เรียกว่า overtones พวกเขาเป็นคนที่ก่อให้เกิดเสียงต่ำทำให้สามารถแยกไวโอลินจากเปียโนและกีตาร์จากแซกโซโฟน พวกเขาไม่อนุญาตให้สับสนเสียงชายและหญิงหรือแยก Petrov จาก Ivanov และไซน์อยด์เท่านั้นที่ไม่สามารถสลายตัวหรือประกอบจากสัญญาณใด ๆ อีกต่อไป

รูปที่ 2 แสดงโครงสร้างของพัลส์รูปสี่เหลี่ยมผืนผ้า

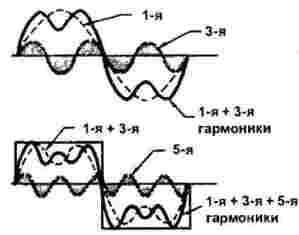
รูปที่ 2

เสียงประสานที่หนึ่งและที่สามจะแสดงในส่วนบนของรูป มันง่ายที่จะเห็นว่าในช่วงเวลาหนึ่งของสามช่วงแรกของฮาร์มอนิกสามผ่าน ในกรณีนี้แอมพลิจูดของฮาร์โมนิที่สามคือหนึ่งในสามของแรก จำนวนรวมของฮาร์โมนิกที่หนึ่งและที่สามก็แสดงไว้ที่นี่เช่นกัน

ด้านล่างพร้อมกับผลรวมของฮาร์โมนิก 1 และ 3 ฮาร์มอนิกอีก 5 ตัวจะถูกแสดง: สำหรับช่วงเวลาของสัญญาณรูปสี่เหลี่ยมผืนผ้าที่มันจัดการเพื่อทำห้าจุด ในกรณีนี้แอมพลิจูดของมันจะเล็กลงอย่างแม่นยำยิ่งขึ้น 1/5 ของหลัก (อันแรก) อย่างใดอย่างหนึ่ง แต่ไม่ควรคิดว่าทุกอย่างจะจบลงที่ฮาร์มอนิกห้า: มันไม่สามารถแสดงให้เห็นได้ในรูปที่จริงมีมากกว่านั้น

การก่อตัวของฟันเลื่อยและสัญญาณรูปสามเหลี่ยมที่แสดงในรูปที่ 3 นั้นค่อนข้างซับซ้อนกว่านี้หากในกรณีก่อนหน้านี้มีเพียงเสียงประสานที่แปลก ๆ เท่านั้นที่เข้ามามีส่วนร่วม

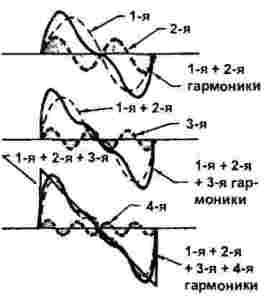
รูปที่ 3

ดังนั้นเราสามารถระบุความจริงที่ว่าด้วยความช่วยเหลือของฮาร์มอนิกหลาย ๆ สัญญาณที่มีการสังเคราะห์รูปร่างใด ๆ และจำนวนและประเภทของฮาร์มอนิกขึ้นอยู่กับรูปคลื่นที่แสดงในรูปที่ 2 และ 3

เมื่อทำการซ่อมและตั้งค่าอุปกรณ์อิเลคทรอนิกส์จะใช้ออสซิลโลสโคปเพื่อศึกษาสัญญาณไฟฟ้า จะช่วยให้คุณพิจารณารูปแบบของสัญญาณเป็นระยะความกว้างของพวกเขาวัดระยะเวลาการทำซ้ำ แต่เสียงประสานที่แสดงในรูปที่ 2 และ 3 ไม่สามารถมองเห็นได้

แม้ว่าคุณจะเชื่อมต่อเช่นกีตาร์ไฟฟ้ากับออสซิลโลสโคปดึงหนึ่งสายไซนัสที่ปรากฏบนหน้าจอก็ยังเป็นฮาร์โมนิแรก ในกรณีนี้จะไม่มีการพูดถึง overtones ใด ๆ ไซน์อยด์เดียวกันจะส่งผลถ้าคุณเป่าเข้าไปในท่อหรือฟลูตที่ด้านหน้าไมโครโฟน

วิธีรับแรงกระตุ้นรูปสี่เหลี่ยมผืนผ้า

หลังจากทำความคุ้นเคยกับสัญญาณไฟฟ้าเราจำเป็นต้องเรียกคืนตัวเก็บประจุที่บทความเริ่มต้นขึ้น ก่อนอื่นคุณควรทำความคุ้นเคยกับหนึ่งในวงจรอิเล็กทรอนิกส์คลาสสิค - multivibratorมันคือผู้ที่สร้างพัลส์รูปสี่เหลี่ยมผืนผ้า วงจรเป็นแบบคลาสสิคที่เริ่มทำงานได้ทันทีโดยไม่ต้องตั้งค่าหรือปรับแต่งใด ๆ

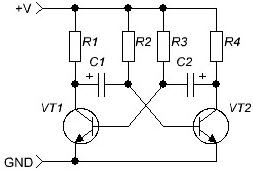
รูปที่ 4

มัลติฟังก์ชั่นเป็นแอมพลิฟายเออร์สองระดับที่ครอบคลุมโดยการตอบรับเชิงบวก หากตัวต้านทานโหลดสะสมตัวเก็บรวบรวม R1 = R4 ตัวต้านทานพื้นฐาน R2 = R3 และตัวเก็บประจุ C1 = C2 มีค่าเท่ากันมัลติวิเบรเตอร์เรียกว่าสมมาตรและสร้างพัลส์คลื่นสี่เหลี่ยมของประเภทคดเคี้ยว - ระยะเวลาพัลเท่ากับระยะเวลาหยุดชั่วคราว

รอบการทำงานของพัลส์ดังกล่าว (อัตราส่วนของช่วงเวลาต่อช่วงเวลาพัลส์) เท่ากับสอง ในรูปแบบภาษาอังกฤษทุกอย่างตรงกันข้าม: พวกเขาเรียกว่ารอบการทำงาน มันถูกคำนวณเป็นอัตราส่วนของระยะเวลาการเต้นของชีพจรต่อระยะเวลาของการสืบทอดและแสดงเป็นเปอร์เซ็นต์ ดังนั้นสำหรับเส้นทางคดเคี้ยวรอบหน้าที่ 50%

คอมพิวเตอร์ถูกต้องหรือไม่

multivibrator ชื่อถูกเสนอโดยนักฟิสิกส์ชาวดัตช์ van der Pol เนื่องจากสเปกตรัมของสัญญาณรูปสี่เหลี่ยมผืนผ้ามีฮาร์โมนิคจำนวนมาก คุณสามารถตรวจสอบสิ่งนี้หากคุณสามารถวางเครื่องรับวิทยุไว้ในช่วงคลื่นกลางใกล้กับเครื่องปรับความถี่ที่ใช้งานได้แม้ในความถี่เสียง: เสียงโหยหวนจะมาจากลำโพง สิ่งนี้ชี้ให้เห็นว่านอกเหนือจากความถี่เสียงเครื่องขยายสัญญาณความถี่ยังปล่อยสัญญาณความถี่สูง

เพื่อกำหนดความถี่ในการสร้างเราสามารถใช้สูตร f = 700 / (C1 * R2)

ด้วยรูปแบบของสูตรนี้ความจุของตัวเก็บประจุในไมโครโฟโต้ (μF) ความต้านทานเป็นกิโลโอห์ม (KΩ) ผลลัพธ์เป็นเฮิร์ตซ์ (Hz) ดังนั้นความถี่จะถูกกำหนดโดยค่าคงที่เวลาของวงจร C1 * R2 การโหลดตัวเก็บรวบรวมจะไม่มีผลกับความถี่ ถ้าเราใช้ C1 = 0.02 μF, R2 = 39 KΩดังนั้นเราจะได้ f = 700 / (0.02 * 39) = 897.4 Hz

Multivibrator ในยุคของคอมพิวเตอร์และ ไมโครคอนโทรลเลอร์ ตามรูปแบบนี้มันแทบจะไม่เคยใช้ถึงแม้ว่ามันอาจจะเหมาะสำหรับการทดลองที่หลากหลาย ก่อนอื่นใช้คอมพิวเตอร์ นี่คือลักษณะของวงจรรวมเครื่องปรับคลื่นความถี่ในโปรแกรม Multisim การเชื่อมต่อของออสซิลโลสโคปก็แสดงไว้ที่นี่เช่นกัน

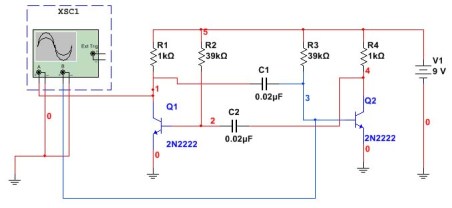
รูปที่ 5

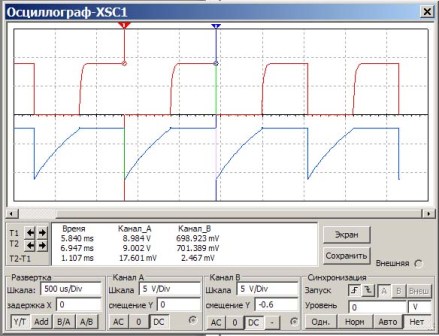
ในวงจรนี้ตัวเก็บประจุและตัวต้านทานจะถูกติดตั้งตามตัวอย่างก่อนหน้านี้ งานคือการตรวจสอบการคำนวณตามสูตรว่าจะได้รับความถี่เดียวกันหรือไม่ เมื่อต้องการทำเช่นนี้วัดระยะเวลาของพัลส์แล้วคำนวณใหม่ในความถี่ ผลลัพธ์ของ Multisim oscilloscope แสดงในรูปที่ 6

รูปที่ 6

คำอธิบายบางอย่างเพื่อรูปที่ 6

บนหน้าจอออสซิลโลสโคปชีพจรสีแดงแสดงพัลส์บนตัวสะสมทรานซิสเตอร์และสีน้ำเงินบนฐาน ด้านล่างในหน้าจอในหน้าต่างสีขาวขนาดใหญ่ตัวเลขแสดงผลการวัด เราสนใจคอลัมน์“ เวลา” เวลาถูกวัดโดยตัวบ่งชี้ T1 และ T2 (สามเหลี่ยมสีแดงและสีน้ำเงินเหนือหน้าจอ)

ดังนั้นระยะเวลาการทำซ้ำของพัลส์ T2-T1 = 1.107ms จึงถูกแสดงอย่างแม่นยำ มันยังคงเป็นเพียงการคำนวณความถี่ f = 1 / T = 1 / 1.107 * 1000 = 903Hz

ผลลัพธ์เกือบเหมือนในการคำนวณตามสูตรซึ่งให้สูงขึ้นเล็กน้อย

ตัวเก็บประจุสามารถใช้แยกกันไม่ได้เท่านั้น: เมื่อใช้ร่วมกับตัวต้านทานจะช่วยให้คุณสร้างฟิลเตอร์ต่าง ๆ หรือสร้างวงจรการเปลี่ยนเฟส แต่จะกล่าวถึงในบทความถัดไป

ความต่อเนื่องของบทความ: ตัวเก็บประจุในวงจรอิเล็กทรอนิกส์ ส่วนที่ 2

Boris Aladyshkin