Būla algebra. 3. daļa. Kontaktu shēmas

Rakstā aprakstīti releju ķēžu projektēšanas pamatprincipi atbilstoši dotajam to darbības algoritmam.

Divos iepriekšējie raksti tika stāstīts par pamatiem Būla algebra un stafetes algebra. Uz šī pamata tika izstrādātas strukturālās formulas, un uz tām tika izstrādātas jau tipiskas kontaktu shēmas.

Strukturālās formulas sastādīšana pēc gatavas shēmas ir vienkāršs jautājums. Daudz grūtāk ir uzrādīt topošās mašīnas elektrisko ķēdi saskaņā ar gatavu konstrukcijas formulu. Tam nepieciešama apmācība!

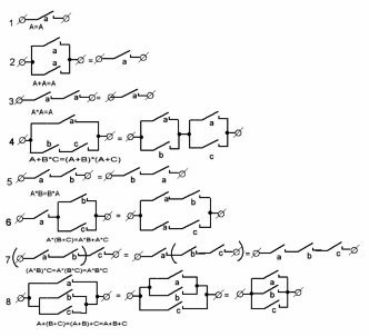
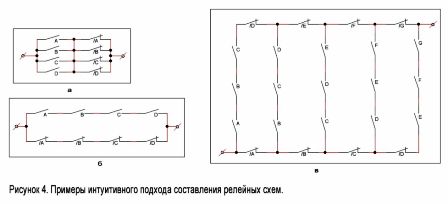
1. attēlā parādītas visizplatītākās iespējas. kontaktu shēmas un to ekvivalenti. Viņi palīdzēs sagatavot mašīnu elektriskās ķēdes, kā arī analizēs gatavas konstrukcijas, piemēram, to remonta procesā.

Kā jūs varat izmantot kontaktu shēmu iespējas, kas apskatītas iepriekš?

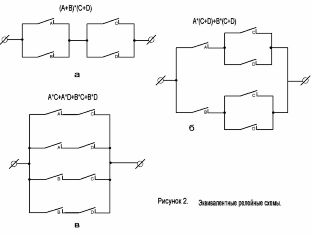
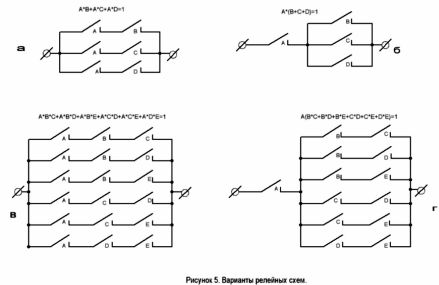
Apsveriet shēmu, kas parādīta 2. attēlā, a. Atbilstošajai struktūras formulai ir šāda forma: (A + B) * (C + D).

Izmantojot Būla algebras sadalījuma likumu, šajā izteiksmē atveram iekavas un iegūstam: A * (C + D) + B * (C + D), kas atbilst shēmai, kas parādīta 2. attēlā, b. Turklāt reizināšanas dēļ mēs varam iegūt formulu A * C + A * D + B * C + B * D, kas atbilst 2. attēlam, c.

Visas trīs shēmas ir līdzvērtīgas, tas ir, tās izrādās slēgtas ar vienādiem nosacījumiem. Tomēr tie atšķiras pēc sarežģītības.

1. attēls. Tipiskas kontaktu shēmas

Pirmajai no shēmām, visvienkāršākajai, ir nepieciešami četri releji, no kuriem katram jābūt vienam parasti atvērtam kontaktam. (Lai vienkāršotu rasējumus, releju spoles netiek parādītas).

Shēmai "b" ir nepieciešams relejs ar divām kontaktu grupām. Kontaktu ķēžu algebra galvenais uzdevums ir atrast visas līdzvērtīgās shēmas, lai no tām varētu izvēlēties vienkāršāko.

2. attēls. Ekvivalentas kontaktu shēmas.

Lai konsolidētu apskatīto materiālu, mēģiniet pats atrisināt šādas problēmas.

1. Uzzīmējiet automātiskā shēmas shēmu ar struktūras formulu A * B * C * D + A * B * E + A * D.

2. Pierādiet, ka shēmas, kas parādītas 3. attēlā, a un b, ir līdzvērtīgas.

3. Vienkāršojiet ķēdi, kas parādīta 3. attēlā, c.

4. Kāda strukturālā formula realizē shēmu 3. attēlā, d?

Pēc tam, ko mēs jau esam izpētījuši, būs iespējams sākt risināt problēmas, kas tika izvirzītas pirmā raksta pašā sākumā. Mēs tos īsi atgādinām.

Pirmais uzdevums bija telpā ieslēgt un izslēgt spuldzi ar trim slēdžiem, kas atrodas dažādās vietās: pie durvīm, pie galda, pie gultas.

Otrais uzdevums ir balsot par sporta tiesnešiem: no četriem tiesnešiem “PAR” ir jānobalso vismaz diviem ar nosacījumu, ka “PAR” balsoja komisijas priekšsēdētājs.

Trešais uzdevums bija paredzēts tikai izglītības vajadzībām. Tas ierosināja tādu pašu kā pirmais, tikai sešiem slēdžiem, it kā telpā būtu sešas sienas. Līdzīgas shēmas tikai tiek izstrādātas, izmantojot releju ķēžu algebru.

Kopumā, ja mēs vēlamies izstrādāt shēmu, kurai ir dažas noteiktas loģiskās īpašības, tad šai problēmai varam pievērsties divos dažādos veidos. Parasti šos ceļus var saukt par “intuitīvajiem” un “algebriskajiem”.

Dažus uzdevumus labāk risina pirmajā veidā, bet citus - otrajā. Intuitīvā pieeja izrādās ērtāka, ja ķēdes darbību kontrolē daudzi slēdži, taču šo releju savstarpējā izvietojumā ir zināma simetrija. Mēs redzēsim, ka šeit intuitīva pieeja mērķa sasniegšanai notiek ātrāk, savukārt releja algebras aparāta izmantošana daudzu mainīgo gadījumā var būt ļoti apgrūtinoša. Ir lietderīgi iepazīties ar abām iespējamām pieejām šīs problēmas risināšanai.

Sāksim ar intuitīvu pieeju. Pieņemsim, ka mums vajadzēja izveidot ķēdi, kas tika slēgta, kad strādāja visas n vadības releja ķēdes.

Šīs problēmas risinājumam nav vajadzīgas ilgas pārdomas: ir skaidrs, ka uzstādītais nosacījums tiks izpildīts, ja tos savstarpēji savienos secīgi n parasti atvērtus releja kontaktus.

Tāpat ir acīmredzams, ka, lai izveidotu ķēdi, kas aizveras, kad vismaz viens no n relejiem ir iedarbinājies, pietiek ar to, lai paralēli pievienotu n parasti atvērtus releja kontaktus.

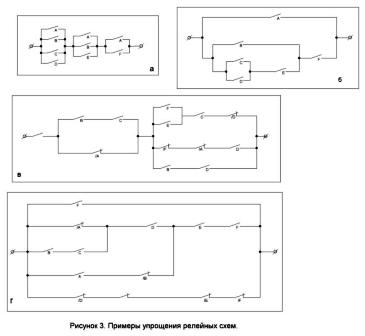
Ir viegli iedomāties ķēdi, kas tiek aizvērta, kad tiek iedarbināti daži, bet ne visi releji. Šāda shēma ir parādīta 4. attēlā, a. Labajā pusē ir diagramma, kas darbojas pēc principa "viss vai nekas". Tas tiks aizvērts tikai tad, kad visi releji ieslēgsies vai releji tiks atvienoti (4., 6. attēls).

Apsveriet tagad sarežģītāku piemēru. Lai ir n kontakti, kas atrodas noteiktā secībā: A, B, C, D, E, F ... Mēs izveidosim ķēdi, kas tiek aizvērta, kad tiek slēgti visi ar k virkni savienotie kontakti, un tikai tie ir. Šāda vērtību n = 7 un k = 3 shēma parādīta 4. attēlā, c. Metode šādu shēmu konstruēšanai jebkurām citām n un k vērtībām ir skaidra no šī attēla.

Mēs turpinām ķēžu konstruēšanu atbilstoši dotajiem viņu darba nosacījumiem, izmantojot releja algebru.

Tāpat kā iepriekš, ķēdes darbības apstākļus vienmēr vispirms nosaka mutiski. Dizaineram, pirmkārt, jāspēj vārdos ievietot to, ko viņš vēlas. Ja viņam nav tik skaidrības, tad neviena algebra nepalīdzēs. Jums vienmēr jāsāk ar skaidru prasību izklāstu, kas noteiktas pirms jaunās shēmas. Kā jebkurā biznesā, šis uzdevums, iespējams, ir visgrūtākais. Ja nosacījumi ir pietiekami vienkārši, tad mēs uzreiz varam uzrakstīt strukturālās formulas izteicienu, kas atbilst šīm prasībām.

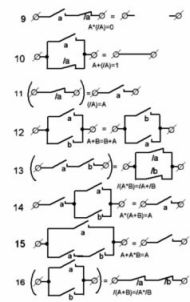
1. piemērs Pieņemsim, ka mums ir jāizveido shēma, kurā ir 4 kontakti A, B, C un D, ​​lai ķēde būtu ieslēgta, kad kontakts A ir aizvērts, un viens no pārējiem trim kontaktiem. Šajā vienkāršajā gadījumā ķēdes darbība verbālā rakstībā izskatīsies šādi: “Ķēdei vajadzētu vadīt strāvu, ja kontakti A un B ir slēgti, vai kontakti A un C vai kontakti A un D. Piekrīt, ka tagad ir ļoti vienkārši sastādīt struktūras formulu. Tas izskatīsies šādi:

A * B + A * C + A * D = 1 vai A * (B + C + D) = 1.

Ķēdei ir divas iespējas. Tie ir parādīti 5. attēlā. Otrajai opcijai nav nepieciešams relejs ar trim parasti atvērtiem kontaktiem.

2. piemērs Pirmais raksts bija 2. uzdevums par sporta tiesnešu balsošanu. Izlasiet rūpīgāk tā stāvokli, tas ir līdzīgs nupat apskatītajam piemēram. Skaidrāks prasību vārdiskais ieraksts izskatīsies šādi: “Ir jāizveido shēma, kurā ir 5 kontakti A, B, C, D, E, lai tā vadītu strāvu un ieslēgtu displeja lampu, ja ir aizvērti šādi kontakti:

A un B un C, vai A un B un D, ​​vai A un B un E, vai A un C un D, ​​vai A un C un E, vai A un D un E. Kontakts A ir priekšsēdētāja poga. Ja tas netiek nospiests, tad katram no 6 loģiskajiem produktiem būs 0, t.i. Balsošana nenotika.

Strukturālā formula būs šāda:

(A * B * C) + (A * B * D) + (A * B * E) + (A * C * D) + (A * C * E) + (A * D * E) = 1,

vai A * (B * C + B * D + B * E + C * D + C * E + D * E) = 1.

Abi shēmas varianti ir parādīti 5., c un d attēlā. Tas ir problēmas risinājums.

Kam ir zināma prasme lasīt strukturālās formulas, ir viegli iedomāties pašas automātikas ķēdi un visas tā iespējas. Interesanti, ka releju ķēžu algebra sniedz vairāk informācijas nekā pat pati ķēde. Tas ļauj jums redzēt, cik daudz un kādi releji ir nepieciešami. Ar tās palīdzību jūs varat viegli atrast ķēdes mašīnas vienkāršāko versiju.

3. piemērs Iegūstot zināmu pieredzi strukturālo formulu sagatavošanā, mēs centīsimies atrisināt sākto problēmu pirmais raksts: jums jāprojektē slēdzis, kas ļauj ieslēgt gaismu, ieejot ieejā, un izslēgt to pēc tam, kad esat uzkāpis uz vēlamās grīdas, vai, tieši otrādi, ieslēdziet to, izejot no dzīvokļa, un izslēdziet pēc tam, kad esat nogājis. Tāda pati situācija notiek garā koridorā: vienā galā spuldzei jābūt iedegtai, bet pēc došanās uz otru galu - jādzēš. Īsāk sakot, uzdevuma mērķis ir kontrolēt vienu spuldzi no dažādām vietām ar diviem slēdžiem.

Problēmas risināšanai mēs izvēlamies šādu procedūru: vispirms skaidri noformulējam slēdžu darbības apstākļus, pēc tam mēs tos uzrakstam formulas formā, un, pamatojoties uz tiem, mēs uzzīmēsim elektrisko ķēdi.

Tā kā spuldze dega (1), ir nepieciešams, lai būtu izpildīts viens no diviem nosacījumiem:

1. Ieslēdziet slēdzi apakšā (A) un izslēdziet augšpusē (/ B). Ieej lievenī.

2. Ieslēdziet slēdzi augšpusē (B) un izslēdziet apakšējo (/ A). Atstājiet dzīvokli.

Izmantojot pieņemto apzīmējumu, strukturālo formulu uzraksta šādi:

A * (/ B) + (/ A) * B = 1

Slēdža shēma ir parādīta 6. attēlā. Pašlaik šādi slēdži ir komerciāli pieejami, tie ir tā sauktie pārslēgšanas slēdži. Tādēļ šo shēmu apsvēršana šeit tiek dota tikai viņu darba vispārīgo principu koncepcijai.

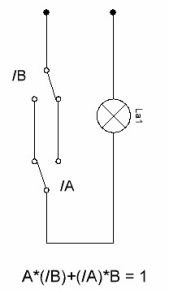
6. attēls

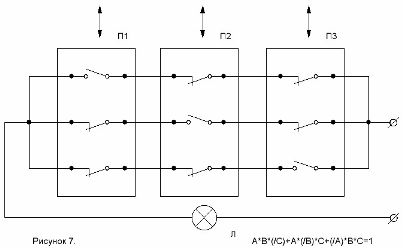
Pirmā raksta sākumā uzdevumā Nr. 1 mēs runājām par shēmu, kas ļauj ieslēgt un izslēgt gaismu telpā ar jebkuru no trim slēdžiem. Spriežot tāpat kā divu slēdžu gadījumā, iegūstam struktūras formulu:

A * B * (/ C) + A * (/ B) + (/ A) * B * C = 1.

Pēc šīs formulas izveidotā shēma ir parādīta 7. attēlā.

7. attēls

Pirmā raksta sākumā tika ierosināts vienkāršs izglītības uzdevums Nr. 2: it kā istabā būtu sešas sienas, un katrai no tām būtu slēdzis. Ķēdes loģika ir tieši tāda pati kā trim slēdžiem. Apzīmēsim tos ar burtiem A, B, C, D, E, F. Atgādinām, ka apzīmējums (/ A), (/ B) un tā tālāk ir nevis dalīšanas zīme, bet loģiska noliegums. Biežāk to norāda ar pasvītrojuma burtiem un, pat veseliem izteicieniem, virsū. Dažās shēmās šo pasvītrojumu vienkārši aizstāj ar mīnusa zīmi. Sešu slēdžu strukturālā formula ir šāda:

(/ A) * B * C * D * E * F + A * (/ B) * C * D * E * F + A * B * (/ C) * D * E * F + A * B * C *

(/ D) * E * F + A * B * C * D * (/ E) * F + A * B * C * D * E * (/ F) = 1.

Lasītāji tiek aicināti sastādīt pilnīgu elektrisko ķēdi, kurā tiek realizēta šī strukturālā formula, lai iegūtu praktiskas iemaņas ķēžu projektēšanā. Neliels padoms: kontūrai jums būs nepieciešami seši releji, no kuriem katram ir viens parasti atvērts kontakts un pieci parasti ir aizvērti. Šādus sarežģītus relejus, ja nepieciešams, var salikt no vairākiem vienkāršākiem, savienojot to spoles paralēli.

Tas noslēdz stāstu par Būla algebru un releju ķēžu algebru.

Raksta turpinājums: Loģikas mikroshēmas

Boriss Aladyshkin