Būla algebra. 2. daļa. Pamatlikumi un funkcijas

Stāsta turpinājums par Būla algebru, konvencijām, noteikumiem, operācijām. Pāreja uz kontaktu shēmu pamatiem.

Iekšā pirmais raksts Džordžs Bulls tika raksturots kā loģikas algebra veidotājs. Otrajā rakstā tiks aprakstītas Būla algebras pamatdarbības un metodes Būla izteiksmju vienkāršošanai. Tātad Būla algebra apgalvojumus izmanto kā argumentus, nevis to nozīmi, bet gan apgalvojuma patiesumu vai nepatiesību.

Forma izteicienu rakstīšanai Būla algebrā.

Ja apgalvojums ir patiess, tad to raksta šādi: A = 1, ja tas ir nepatiess, tad A = 0 (galu galā nav taisnība, ka kartupelis ir auglis). Jebkuram apgalvojumam A ir vai nu patiesa (A = 1), vai nepatiesa (A = 0). Šeit nevar būt vidus. Par to mēs jau runājām.

Ja savienojat divus vienkāršus paziņojumus ar savienību Un, tiek iegūts sarežģīts paziņojums, ko sauc par loģisku produktu. Pieņemsim divus vienkāršus paziņojumus: “Trīs ir vairāk nekā divi” mēs apzīmēsim ar burtu A, “Trīs ir mazāki par pieciem” - ar burtu B.

Tādējādi sarežģītais teiciens “Trīs ir vairāk nekā divi un mazāk nekā pieci” ir loģisks (šajā gadījumā lielais burts I norāda, ka šī ir “UN” loģiska darbība, kā arī vēlāk tekstā “VAI” un “NAV”). un B. to apzīmē šādi: A ^ B vai A * B.

Loģiskā reizināšana (darbība "UN").

Pamata algebrā A * A = A2. Bet Buhla algebrā A * A = A2 = A, A * A = A, jo reizināšanas zīme (*) tagad nozīmē ... Un ... And nozīmē un ... Un. Visa mūsu pieredze apstiprina, ka A&A ir tas pats, kas A. viens pats. Tam nevar nepiekrist. Paziņojuma patiesība nemainās, ja faktors to atkārto vairākas reizes.

Divu apgalvojumu reizinājums tiek uzskatīts par patiesu (vienāds ar 1), un tikai tad, ja abi faktori ir patiesi, un nepatiess (vienāds ar 0), ja vismaz viens no faktoriem ir nepatiess. Piekrītat, ka šie noteikumi nav pretrunā ar veselo saprātu, un turklāt tie pilnībā atbilst elementārās algebras noteikumiem:

1*1 = 1, 1*0 = 0 = 0*1 = 0, 0*0 = 0.

Pirmā vienādība ir šāda: ja gan A, gan B ir patiesas, tad reizinājums A * B ir patiess. Buhla algebrā reizinājuma zīme (*) aizstāj I savienību.

Loģiskajos produktos var būt nevis divi, bet lielāks apgalvojumu skaits - faktori. Un šajā gadījumā produkts ir patiess tikai tad, ja tajā pašā laikā visi apgalvojumi-faktori ir patiesi.

Loģiskais papildinājums (VAI darbība)

Ja divus apgalvojumus savieno savienība VAI. to, kas veido saliktu teikumu, sauc par loģisku summu.

Apsveriet loģiskas summas piemēru. Sakot A: "Šodien es iešu uz kino."

B paziņojums: "Šodien es iešu uz diskotēku." Mēs pievienojam abus paziņojumus un saņemam: "Šodien es iešu uz filmām vai uz diskotēku."

Šis sarežģītais paziņojums tiek apzīmēts šādi: A + B = C vai (A V B) = C.

Ar C mēs apzīmējām sarežģītu loģiskas summas paziņojumu.

Apskatāmajā piemērā savienību VAI nevar izmantot ekskluzīvā nozīmē. Patiešām, tajā pašā dienā jūs varat nokļūt kinoteātrī un diskotēkā. Un šeit ir teiciens:

“Dārzkopības biedrības priekšsēdētājs būs Petrovs vai Ivanovs,” tā nav loģiska summa, jo priekšsēdētājs būs tikai viens cilvēks, bet otrs - parasts dārznieks amatieris.

Zīme V loģiskajai summai ir izvēlēta, jo tā ir latīņu vārda "vel" sākuma burts, kas nozīmē "vai", atšķirībā no latīņu vārda "aut>, kas nozīmē" un ". Tagad visiem vajadzētu būt skaidriem, kāpēc loģisko produktu apzīmē ar zīmi ^.

Pamata algebrā ir noteikums A + A = 2A. Šis noteikums ir taisnība, neatkarīgi no tā, kuru skaitli attēlo burts A. Boolean algebrā tam atbilst noteikums A + A = A. Visa mūsu dzīves pieredze saka, ka pateikt A VAI A vai abi A ir tikai vēl viens un garāks veids, kā pateikt tikai A.

Tāpat kā jebkurš salikts apgalvojums, arī divu apgalvojumu A un B summa var būt patiesa vai nepatiesa. Summa tiek uzskatīta par patiesu, tas ir, vienāda ar vienotību, ja vismaz viens no noteikumiem ir patiess:

A + B = 1, ja VAI A = 1 VAI B = 1, kas atbilst parastajam aritmētiskajam:

1+0 = 0+1 = 1.

Ja abi summētie apgalvojumi ir patiesi, tad arī summa tiek uzskatīta par patiesu, tāpēc Būlijas algebrā mums ir: (1) + (1) = 1.

Iekavās šeit ir iestatīts, lai uzsvērtu nosacījuma, šī papildinājuma nozīmi, nevis aritmētisko.

Divu apgalvojumu summa tiek uzskatīta par nepatiesu un vienāda ar nulli, ja, bet tikai tad, ja abi vārdi ir nepatiesi. No šejienes:

0 + 0=0.

Tātad divu apgalvojumu A + B summa tiek uzskatīta par patiesu, ja patiesa, VAI A, VAI B, VAI abi termini kopā. Tādējādi vārdu VAI apzīmē ar +.

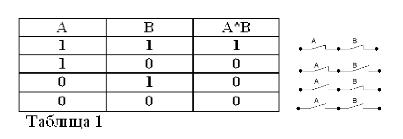
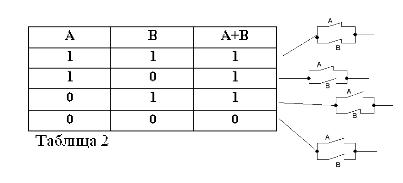
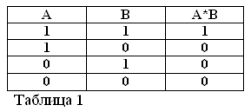
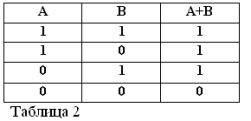
Atceroties, ka apgalvojumi A un B var būt tikai patiesi vai nepatiesi, un tāpēc tiem ir patiesības pakāpe 1 vai 0, apsvērto UN un OR darbību rezultātus var apkopot 1. un 2. tabulā.

Trešā operācija, ko plaši izmanto Buhla algebra, ir negācijas operācija - NAV. Atgādinām, ka elementārā algebra izmanto operācijas ADD, D Atņemt, Reizināt ar, Dalīt ar un dažas citas.

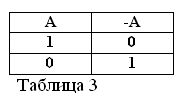
Katram apgalvojumam A ir tā noliegums NAV A, ko mēs apzīmēsim ar simbolu / A. Par to nevajadzētu šaubīties.

Mēs sniedzam piemērus: “Mēs iesim uz mežu” A, “Mēs neiesim uz mežu” / A.

Ja apgalvojums A ir patiess, tas ir, A = 1, tad tā noliegumam / A ir jābūt nepatiesam / A = 0. Un otrādi, ja kāds apgalvojums ir nepatiess, tad tā noliegums ir taisnība. Piemēram: “Zirgs neēd sienu” / A = 0, “Zirgs neēd sienu” (A = 1). To var izteikt 3. tabulā.

Nosakot nolieguma darbības nozīmi un pieņemot, ka diviem apgalvojumiem A un / A vienmēr ir viena taisnība, seko divas jaunas Būla algebras formulas:

A + (/ A) = 1 un A * (/ A) = 0.

Ir arī citas formulas, kas vienkāršo paziņojumu loģisko apstrādi. Piemēram, 1 + A = 1, jo saskaņā ar pievienošanas definīciju gadījumā, ja viens termins ir vienāds ar vienotību, summa vienmēr ir vienāda ar vienotību. Iegūtais rezultāts nav atkarīgs no tā, vai A = 0 vai A = 1.

Katrai no trim pārbaudītajām loģiskajām operācijām (UN, VAI, NAV) ir noteiktas īpašības, kas ir tuvas elementārās algebras noteikumiem. Ja tie visi ir noformulēti, tad mēs iegūstam 25 Būla algebras noteikumus. Tie ir pietiekami, lai atrisinātu gandrīz jebkuru loģisku problēmu. Bez šiem noteikumiem loģisko problēmu šķietamās sarežģītības dēļ kļūst diezgan grūti. Mēģināt atrast pareizo atbildi, neizmantojot noteikumus, nozīmē aizstāt tos ar atjautību un vispārīgu pamatojumu. Noteikumi ievērojami atvieglo šo darbu un ietaupa laiku.

Raksta ietvaros nav iespējams izskatīt visus šos 25 noteikumus, taču tie, kas vēlas, tos vienmēr var atrast attiecīgajā literatūrā.

Kā jau minēts pirmajā rakstā 1938. gadā, jaunais amerikāņu zinātnieks Klods Šenons rakstā “Releju un komutācijas ķēžu simboliskā analīze” pirmo reizi releja tehnoloģijas problēmām izmanto Būla algebru. Šenona atklājums bija tas, ka viņš saprata, ka releju mašīnu un elektronisko datoru projektēšanas metode faktiski ir matemātiskās loģikas filiāle.

Tas bieži notiek. Daudzus gadus zinātnieks strādā pie problēmas, kas viņa tautiešiem šķiet pilnīgi nevajadzīga - vienkārši jautra. Bet paiet gadu desmiti un dažreiz gadsimti, un teorija, kas nevienam nav vajadzīga, ne tikai iegūst tiesības pastāvēt, bet bez tā turpmāka attīstība kļūst neiedomājama.

Kas palīdzēja Šenonai otro reizi “atklāt” Būla algebru? Lieta? Nekāda veida.

Releju mašīnu mīlestība, kas veidota uz parastajiem slēdžiem un relejiem, jaunajam zinātniekam palīdzēja savienot aizmirstu teoriju ar automātisko telefona centrāļu uzdevumiem, pie kuriem viņš tajā laikā strādāja. Pēc tam Šenons ieviesa to pašu ideju “jā vai nē” diskrētos ziņojumos un lika pamatus veselai kibernētikas sadaļai - informācijas teorijai.

Buhla algebra bija ļoti piemērota releju ķēžu analīzei un sintēzei. Tas bija pietiekami, lai pieņemtu kā patiesu paziņojumu: “Ķēdē ir signāls”, un kā nepatiesu - “Ķēdē nav signāla”, jo parādījās jauna algebra - signāla algebra, releja ķēdes algebra.

Jaunā algebra ir derīga tikai releju un komutācijas ķēžu ņemšanai vērā. Galu galā tikai šādās shēmās ir izpildīti nosacījumi “ir signāls” un “nav signāla”. Ja signāls nepārtraukti mainās, iegūstot patvaļīgi lielu skaitu starpposmu apstākļu (šādu signālu sauc par analogo), releja algebra nav piemērojama. Tas vienmēr ir jāatceras. Bet tikai vairums elektronisko datoru un kibernētisko mašīnu izmanto diskrētu signāla apstrādes principu, kas balstās uz elementiem “jā - nē”.

Izteicienu “Kontakts ir slēgts” Šenons pieņēma kā patiesu (1) un “Kontakts ir atvērts” kā nepatiesu (0). Pārējo "algebras" daļu, ieskaitot operācijas UN, OR un NOT un 25 noteikumus, Šenons aizņēmās no Būla.

Releju shēmas algebra izrādījās vienkāršāka nekā Būla algebra, jo tā attiecas tikai uz "jā - nē" tipa elementiem. Turklāt jaunā algebra ir vizuālāka.

Šīs algebras elementi ir kontakti, kurus mēs apzīmēsim ar burtiem A, B, C ... Kontakts ir slēgts - A, kontakts ir atvērts - / A (burts ar domuzīmi).

Apzīmējums, kā redzat, ir pilnībā ņemts no Būla algebras. Atvērts kontakts ir slēgta kontakta noliegums. Tas pats kontakts nevar būt gan slēgts, gan atvērts.

Mēs piekrītam, ka, ja kādā ķēdē divus kontaktus apzīmē ar vienu un to pašu burtu, tas nozīmē, ka tiem vienmēr ir vienādas vērtības.

Jebkurā brīdī tie ir vai nu abi vienlaikus atvērti, vai arī abi ir slēgti. Vienkāršākais veids, kā iedomāties tos mehāniski savienotus kopā, lai abi vienlaikus atvērtu vai aizvērtu.

Ja kādā ķēdē kontakts ir cita kontakta noliegums, tad to nozīme vienmēr ir pretēja. Piemēram, kontakti C un / C nekad nevar būt vienlaikus atvērti vai vienlaicīgi aizvērti. Un diagrammā tos var attēlot mehāniski savienotus: ja viens no tiem atveras, tad otrs aizveras.

Mēs sākam iepazīšanos ar releju algebru, analizējot vienkāršākās shēmas, kas atbilst operācijām AND, OR un NOT.

Divu kontaktu (darbība UN) reizinājums ir ķēde, kas iegūta to virknes savienojuma rezultātā: tā tiek aizvērta (vienāda ar 1) tikai tad, kad abi kontakti ir aizvērti (vienāds ar 1).

Divu kontaktu (VAI darbība) summa būs shēma, kas izveidojas, kad tie ir savienoti paralēli: tā ir slēgta (vienāda ar 1), kad vismaz viens no kontūru veidojošajiem kontaktiem ir slēgts (vienāds ar 1).

Šī kontakta pretstats (darbība NAV) ir kontakts, kas vienāds ar 0 (atvērts), ja šis kontakts ir 1 (slēgts), un otrādi.

Tāpat kā Būla algebrā, ja kontaktus apzīmē ar burtiem A un B, tad divu kontaktu rezultātu apzīmēsim ar A * B, summu ar A + B un kontaktu, kas atrodas pretī A, ar / A. Iepriekš paskaidrots 1., 2. un 3. attēlā.

Tabulu derīgums, kas atbilst operācijām AND, OR un NOT. tagad nevienam nevajadzētu šaubīties.

Ļaujiet mums pakavēties pie diviem piemēriem: 1 * 0 = 0 un 1 + 0 = 1.

No attēla redzams, ka pastāvīgi slēgts kontakts, kas virknē savienots ar pastāvīgi atvērtu kontaktu, ir līdzvērtīgs pastāvīgi atvērtam kontaktam (1 * 0 = 0) Pastāvīgi slēgts kontakts, kas savienots paralēli pastāvīgi atvērtam kontaktam, ir līdzvērtīgs pastāvīgi slēgtam kontaktam.

Iepazīstoties ar kontaktu ķēžu aritmētiku, jūs varat aprakstīt jebkuru releja ķēdi ar formulu, izmantojot pieņemtās konvencijas. Kibernētikā šādas formulas sauc par strukturālām.

Ja jebkuras releja shēmas strukturālā formula ir 1, tad caur to var iziet signāls - ķēde ir aizvērta. Un otrādi, ja ķēdes strukturālā formula ir 0, signāls caur to netiks cauri - ķēde ir salauzta.Secinājums: divas releju shēmas ir līdzvērtīgas viena otrai, ja to struktūras formulas ir vienādas.

Raksta turpinājumā mēs apskatīsim kontaktu ķēžu, tipisko kontaktu ķēžu un to ekvivalentu piemērus, kā arī sastādīsim diagrammas pēc struktūras formulām. Mēs arī uzskatām galvenās loģiskās shēmas, kas pilda Būla algebras funkcijas.

Raksta turpinājums: Būla algebra. 3. daļa. Kontaktu shēmas

Boriss Aladyshkin