Kondenzátory v elektronických obvodech

V předchozích článcích jsme stručně hovořili o činnosti kondenzátorů v střídavých obvodech, o tom, jak a proč kondenzátory propouštějí střídavý proud (viz - Kondenzátory střídavého proudu) V tomto případě se kondenzátory nezahřívají, energie jim není přidělena: v jedné polovině vlny sinusoidu se kondenzátor nabije a ve druhém se přirozeně vybije, zatímco přenáší uloženou energii zpět do zdroje proudu.

Tento způsob předávání proudu vám umožňuje volat kondenzátor jako volný odpor, a proto kondenzátor připojený k zásuvce nečiní otáčení čítače. A to vše proto, že proud v kondenzátoru je přesně před 1/4 času, kdy na něj bylo aplikováno napětí.

Ale tento fázový postup umožňuje nejen „trik“ čítače, ale umožňuje také vytvářet různé obvody, například generátory sinusových a pravoúhlých signálů, časové zpoždění a různé frekvenční filtry.

V průběhu tohoto příběhu bude třeba si někdy vzpomenout na to, co již bylo řečeno, abych to shrnul. Pomůže to nevrátit se k předchozím článkům, abychom si vzpomněli na jednoduchý vzorec nebo jednoduše „co je to?“

Paralelní a sériové zapojení kondenzátorů

Při paralelním připojení kondenzátorů je celková kapacita jednoduše aritmetickým součtem kapacit. Při tomto zahrnutí bude přirozeně celková kapacita větší než kapacita největšího kondenzátoru. Ctotal = C1 + C2 + C3 + ... + Cn.

V případě sériového připojení je celková kapacita menší než kapacita nejmenší.

1 / Celkový součet = 1 / C1 + 1 / C2 + 1 / C3 + ... + 1 / Cn.

Když jsou dva identické kondenzátory zapojeny do série, bude celková kapacita rovna polovině kapacity jednoho: například při připojení dvou kondenzátorů po 1 uF bude celková kapacita 0,5 uF.

Kapacita Xc

Zde je vše, jako při připojování rezistorů, pravý opak: sériové připojení snižuje celkovou kapacitu, zatímco paralelní ji zvyšuje. Tuto okolnost nelze zapomenout při připojování kondenzátorů, protože zvýšení kapacity vede ke snížení kapacity Xc

Xc = 1/2 * π * f * C.

Z pohledu matematiky je to docela přirozené, protože kapacita C je ve jmenovateli zlomku. Mimochodem, frekvence f je na stejném místě, takže zvýšení frekvence také vede ke snížení kapacity Xc. Fyzický význam tohoto je to, že přes stejný kondenzátor je lepší, více bez překážek, že procházejí vysoké frekvence. To bude diskutováno o něco později, pokud jde o dolní a horní propust.

Pokud vezmeme kondenzátor s kapacitou 1 μF, pak pro frekvenci 60 Hz bude jeho Xc 2653 Ohmů a pro frekvenci 400 Hz má stejný kondenzátor Xc pouze 398 Ohmů. Ti, kteří si přejí, mohou tyto výsledky zkontrolovat pomocí vzorce, který nahradí π = 3,14, frekvenci v hertzech a kapacitu v faradech. Výsledek pak bude v ohmech. Vše musí odpovídat systému SI!

Kondenzátory se však nepoužívají pouze jako tlumicí odpory s volným tlumením nebo jako filtry usměrňovače. Bez jejich účasti obvody pro nízkofrekvenční a vysokofrekvenční generátory, různé převodníky tvaru vlny, rozlišovací a integrační obvody, zesilovače a další schémata.

Dále budou zvažovány různé elektrické signály, se kterými kondenzátory musí pracovat. Nejprve to jsou periodické signály vhodné pro pozorování pomocí osciloskop.

Období a frekvence kmitání

Periodická oscilace se proto nazývá periodická, která bez zastavení opakuje stejnou formu, například jednu sinusovou oscilaci. Doba trvání tohoto úplného kolísání se přesně nazývá perioda T a měří se v sekundách, milisekundách, mikrosekundách.Moderní elektronika se dokonce zabývá nanosekundami (miliardtina sekundy).

Počet period za sekundu se nazývá frekvence (jak často) kmitání f a vyjadřuje se v hertzech. 1Hz je frekvence, při které se provádí jedna oscilace, jedna plná perioda za 1 sekundu. Poměr periody a frekvence je vyjádřen jednoduchým vzorcem T = 1 / f.

V souladu s vědomím oscilační periody je tedy velmi snadné vypočítat frekvenci f = 1 / T.

Takto se vypočítá frekvence při měření pomocí osciloskopu: vypočítá se počet buněk v periodě vynásobený dobou trvání jedné buňky a periodu se získá například v mikrosekundách. A aby zjistili frekvenci, jednoduše použili poslední vzorec.

Obyčejné elektronický osciloskop Umožňuje sledovat pouze periodické signály, které lze synchronizovat s frekvencí rozmítání za účelem získání statického obrazu vhodného pro výzkum. Pokud odešlete signál do hudebního programu na vstup osciloskopu, nebudete moci zastavit obraz pro nic. K pozorování takových signálů se používají paměťové osciloskopy.

Když je perioda měřena v milisekundách, je frekvence získávána v kilohertz, pro periodu měřenou v mikrosekundách je frekvence již vyjádřena v megahertzech. To je, pokud nedodržíte požadavky systému SI: perioda v sekundách, frekvence v hertzech.

Nesinusoidální vibrace

Jak již bylo zmíněno dříve, sinusová vlna je nejběžnější a nejvhodnější pro studium a praktické využití periodické křivky. V průmyslových podmínkách se získává pomocí elektrických generátorů, například ve vodních elektrárnách. V elektronických zařízeních se používají vibrace nejrůznějších tvarů.

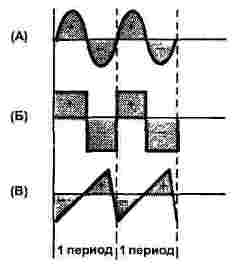
V zásadě se jedná o tři formy: sinusové, pravoúhlé a trojúhelníkové, jak je znázorněno na obrázku 1. Jak proud, tak i napětí mohou mít takový tvar, proto obrázek ukazuje pouze časovou osu, svislá osa je ponechána bez názvu.

Takové oscilace jsou generovány speciálními elektronickými obvody. Obdélníkové a trojúhelníkové signály se často nazývají pulzní. Existuje však řada elektronických obvodů, které provádějí převod signálu: například obdélník, trojúhelník může být vyroben ze sinusoidu.

Obrázek 1

U všech tří signálů obrázek ukazuje dvě periody, všechny signály mají stejnou frekvenci.

Spektrum nesinusových signálů

Jakýkoli elektrický signál může být reprezentován jako měření amplitudy v určitém časovém bodě. Frekvence těchto vzorků se nazývá vzorkovací frekvence a nejméně dvakrát vyšší než horní frekvence měřeného signálu. Poté z těchto vzorků můžete obnovit původní signál. Tato metoda se používá například při digitálním záznamu zvuku. Tato metoda se také nazývá časová analýza.

Jiná metoda předpokládá, že jakýkoli signál, i obdélníkový, může být reprezentován jako algebraický součet sinusoidů s různými frekvencemi a fázemi. Tato metoda se nazývá frekvenční analýza. To, co bylo řečeno „s různými kmitočty“, však není úplně pravda: základní sinusoidy se nazývají harmonické a jejich frekvence se řídí určitými zákony.

Sinusová vlna, jejíž frekvence se rovná frekvenci čtvercové vlny, se nazývá základní nebo první harmonická. Rovnoměrné harmonické jsou získány vynásobením základní frekvence sudým číslem a lichými harmonickými, respektive lichými.

Pokud tedy první harmonická má frekvenci 1 000 Hz, pak druhá je 2 000 Hz, čtvrtá je 4 000 Hz atd. Odd harmonické budou mít frekvence 3000 Hz, 5000 Hz. Navíc, každá harmonická má menší amplitudu než hlavní: čím vyšší je harmonická, tím menší je amplituda.

V hudbě se harmonické nazývají podtóny. Jsou to oni, kdo vytvářejí zvukovou stopu, umožňují rozlišit housle od klavíru a kytaru od saxofonu. Nedovolují zaměňovat mužský a ženský hlas ani rozlišovat Petrov od Ivanov. A pouze sinusoid samotný již nemůže být rozložen nebo sestaven z žádných signálů.

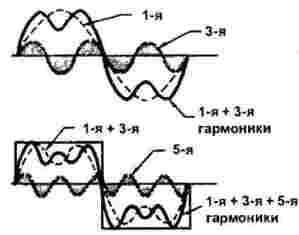
Obrázek 2 ukazuje konstrukci pravoúhlého pulsu.

Obrázek 2

První a třetí harmonické jsou zobrazeny v horní části obrázku. Je snadné vidět, že v jedné periodě první harmonické tři periody třetího průchodu. V tomto případě je amplituda třetí harmonické jedna třetina první. Zde je také uveden součet první a třetí harmonické.

Níže, spolu se součtem 1 a 3 harmonických, je zobrazeno dalších 5 harmonických: za periodu obdélníkového signálu se podaří udělat přesně pět period. V tomto případě je jeho amplituda ještě menší, přesněji 1/5 hlavního (prvního). Člověk by si však neměl myslet, že vše končí pátou harmonickou: na obrázku prostě není možné vše ukázat, ve skutečnosti je jich mnohem víc.

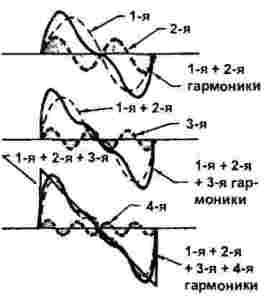
Tvorba pilových a trojúhelníkových signálů, znázorněných na obrázku 3, je poněkud komplikovanější, pokud se v předchozím případě účastnily pouze liché harmonické, začnou hrát i harmonické.

Obrázek 3

Můžeme tedy konstatovat, že pomocí mnoha harmonických je syntetizován signál jakéhokoli tvaru a počet a typ harmonických závisí na tvaru vlny, jak je znázorněno na obrázcích 2 a 3.

Při opravách a nastavování elektronických zařízení se osciloskop používá ke studiu elektrických signálů. To vám umožní zvážit formu periodických signálů, jejich amplitudu, změřit dobu opakování. Harmonické hodnoty znázorněné na obrázcích 2 a 3 však nelze vidět.

I když například připojíte elektrickou kytaru k osciloskopu, zatáhnete za jeden řetězec, na obrazovce se objeví sinusoid, jedná se o první harmonický. V tomto případě nelze hovořit o žádných podtextech. Stejný sinusoid bude mít za následek, pokud vyhodíte do potrubí nebo flétnu před mikrofon.

Jak získat obdélníkové impulsy

Poté, co se seznámíme s elektrickými signály, musíme si vzpomenout na kondenzátory, se kterými byl článek zahájen. Nejprve byste se měli seznámit s jedním z klasických elektronických obvodů - multivibrátor, (Obrázek 4) generuje pravoúhlé pulzy. Obvod je tak klasický, že ihned pracuje, aniž by vyžadoval jakékoli nastavení nebo úpravy.

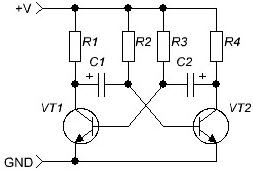
Obrázek 4

Multivibrátor je dvoustupňový zesilovač, pokrytý pozitivní zpětnou vazbou. Pokud jsou zátěžové rezistory R1 = R4, základní rezistory R2 = R3 stejné a kondenzátory C1 = C2 jsou stejné, multivibrátor se nazývá symetrický a generuje pulzy čtvercové vlny typu meandru - doba trvání impulsu se rovná době trvání pauzy.

Pracovní cyklus takových pulzů (poměr periody k trvání pulsu) je roven dvěma. V systémech v anglickém jazyce je všechno přesně opačné: nazývají to pracovní cyklus. Vypočítá se jako poměr doby trvání pulsu k období jeho posloupnosti a je vyjádřen v procentech. Pro meandr je tedy pracovní cyklus 50%.

Je počítač správný?

Název multivibrátor navrhl nizozemský fyzik van der Pol, protože spektrum obdélníkového signálu obsahuje mnoho harmonických. Můžete to ověřit, pokud můžete umístit rádiový přijímač pracující v rozsahu středních vln v blízkosti multivibrátoru, který pracuje i při zvukové frekvenci: vytí přijde z reproduktoru. To naznačuje, že kromě zvukové frekvence multivibrátor také emituje vysokofrekvenční oscilace.

Pro stanovení generační frekvence lze použít vzorec f = 700 / (C1 * R2).

S touto formou vzorce je kapacita kondenzátoru v mikrofaradách (μF), odpor v kiloohmech (KΩ), výsledek v hertzech (Hz). Frekvence je tedy určena časovou konstantou obvodu C1 * R2, zatížení kolektoru neovlivňují frekvenci. Pokud vezmeme C1 = 0,02 μF, R2 = 39 KΩ, dostaneme f = 700 / (0,02 * 39) = 897,4 Hz.

Multivibrátor ve věku počítačů a mikrokontroléry Podle tohoto schématu se téměř nikdy nepoužívá, i když může být vhodný pro různé experimenty. Nejprve pomocí počítačů. Takto vypadá obvod multivibrátoru sestavený v programu Multisim. Zde je také znázorněno spojení osciloskopu.

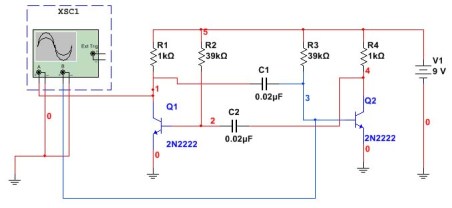
Obrázek 5

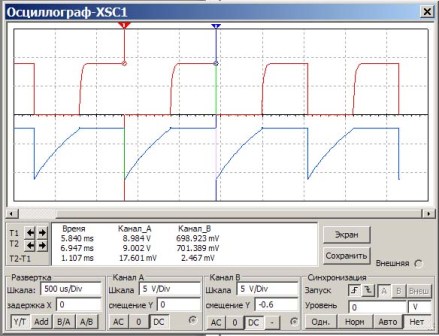
V tomto obvodu jsou kondenzátory a rezistory nainstalovány jako v předchozím příkladu. Úkolem je zkontrolovat výpočet podle vzorce, zda bude dosaženo stejné frekvence. Chcete-li to provést, změřte periodu impulzů a poté je přepočítejte na frekvenci. Výsledek osciloskopu Multisim je znázorněn na obrázku 6.

Obrázek 6

Některá vysvětlení k obrázku 6.

Na obrazovce osciloskopu zobrazuje červený puls pulzy na kolektoru tranzistoru a modrý na základnách. Pod displejem ve velkém bílém okně čísla ukazují výsledky měření. Zajímá nás sloupec „Čas“. Čas se měří pomocí indikátorů T1 a T2 (červené a modré trojúhelníky nad obrazovkou).

Perioda pulzního opakování T2-T1 = 1,107ms je tedy zobrazena docela přesně. Zbývá pouze vypočítat frekvenci f = 1 / T = 1/1 107 * 1 000 = 903 Hz.

Výsledek je téměř stejný jako ve výpočtu podle vzorce, který je uveden o něco vyšší.

Kondenzátory lze použít nejen samostatně: v kombinaci s rezistory umožňují jednoduše vytvářet různé filtry nebo vytvářet obvody fázového posunu. Ale to bude diskutováno v dalším článku.

Pokračování článku: Kondenzátory v elektronických obvodech. Část 2

Boris Aladyshkin