Měření osciloskopu

Digitální osciloskop je samozřejmě mnohem dokonalejší než běžný elektronický, umožňuje zapamatovat si průběhy, může se připojit k osobnímu počítači, má matematické zpracování výsledků, značky obrazovky a mnohem více. Ale se všemi výhodami mají tato zařízení nové generace jednu významnou nevýhodu - to je vysoká cena.

Právě ona dělá digitální osciloskop nepřístupným pro amatérské účely, i když existují „kapesní“ osciloskopy v hodnotě jen několika tisíc rublů, které se prodávají na Aliexpressu, ale není zvlášť vhodné je používat. No, jen zajímavá hračka. Proto budeme hovořit o měřeních pomocí elektronického osciloskopu.

Na téma výběru osciloskopu pro použití v domácí laboratoři na internetu najdete dostatečný počet fór. Aniž bychom popírali výhody digitálních osciloskopů, doporučuje se na mnoha fórech zvolit jednoduché, malé a spolehlivé domácí osciloskopy C1-73 a C1-101 a podobně, s nimiž jsme se dříve setkali tento článek.

Tato zařízení vám za poměrně dostupnou cenu umožní provádět většinu amatérských rádiových úkolů. Mezitím se seznámíme s obecnými principy měření pomocí osciloskopu.

Obrázek 1. Osciloskop S1-73

Co osciloskop měří

Měřený signál je přiváděn na vstup vertikálního vychylovacího kanálu Y, který má velký vstupní odpor, obvykle 1MΩ, a malou vstupní kapacitu, nejvýše 40pF, což umožňuje zavedení minimálního zkreslení do měřeného signálu. Tyto parametry jsou často označeny vedle vstupu vertikálního vychylovacího kanálu.

Obrázek 2. Osciloskop C1-101

Pro vstupní voltmetry je typická vysoká vstupní impedance, takže lze bezpečně říci, že osciloskop měří napětí. Použití externích vstupních děličů vám umožňuje snížit vstupní kapacitu a zvýšit vstupní impedanci. Snižuje také vliv osciloskopu na zkoumaný signál.

Je třeba si uvědomit, že existují speciální vysokofrekvenční osciloskopy, jejichž vstupní impedance je pouze 50 ohmů. V amatérské rozhlasové praxi taková zařízení nenajdou aplikaci. Proto se budeme dále zaměřovat konvenční univerzální osciloskopy.

Šířka pásma kanálu Y

Osciloskop měří napětí ve velmi širokém rozsahu: od stejnosměrného napětí po napětí dostatečně vysoké frekvence. Kolísání napětí může být velmi rozdílné, od desítek milivoltů po desítky voltů a při použití externích děličů až po několik set voltů.

Je třeba mít na paměti, že šířka pásma kanálu vertikální odchylky Y db nejméně 5krát vyšší než frekvence měřeného signálu. To znamená, že zesilovač vertikální odchylky musí projít alespoň pátou harmonickou sledovaného signálu. To je zvláště nutné při studiu pravoúhlých pulzů, které obsahují mnoho harmonických, jak je znázorněno na obrázku 3. Pouze v tomto případě se na obrazovce získá obraz s minimálním zkreslením.

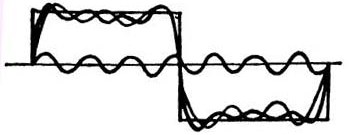
Obrázek 3. Syntéza pravoúhlého signálu z harmonických složek

Kromě základní frekvence je na obr. 3 znázorněna třetí a sedmá harmonická. Jak se harmonické číslo zvyšuje, jeho frekvence se zvyšuje: frekvence třetí harmonické je třikrát vyšší než základní, pátá harmonická je pětkrát, sedmá je sedm atd. V souladu s tím se amplituda vyšších harmonických snižuje: čím vyšší je harmonické číslo, tím nižší je jeho amplituda. Pouze pokud zesilovač vertikálního kanálu bez velkého útlumu může vynechat vyšší harmonické, bude obraz pulsu obdélníkový.

Obrázek 4 ukazuje průběh meandru s nedostatečnou šířkou pásma kanálu Y.

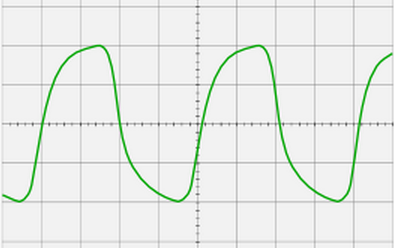
Obrázek 4

Meandr s frekvencí 500 kHz vypadá něco podobného na obrazovce osciloskopu OMSh-3M s šířkou pásma 0 ... 25 kHz. Jako by obdélníkové pulzy procházely integrujícím RC obvodem. Takový osciloskop byl vyroben sovětským průmyslem pro laboratorní práci ve výuce fyziky na školách. I napájecí napětí tohoto zařízení z bezpečnostních důvodů nebylo 220, ale pouze 42V. Je zcela zřejmé, že osciloskop s takovou šířkou pásma umožní pozorovat signál s frekvencemi nepřesahujícími 5 kHz a téměř bez zkreslení.

Pro konvenční univerzální osciloskop je šířka pásma nejčastěji 5 MHz. I s takovým pásmem můžete vidět signál až do 10 MHz a vyšší, ale obraz přijímaný na obrazovce vám umožňuje posoudit pouze přítomnost nebo nepřítomnost tohoto signálu. Bude obtížné říci cokoli o jeho tvaru, ale v některých situacích tvar není tak důležitý: například existuje generátor sinusové vlny a stačí se jen ujistit, že tato sinusová vlna existuje nebo ne. Právě taková situace je na obrázku 4.

Moderní počítačové systémy a komunikační linky pracují na velmi vysokých frekvencích, řádově stovek megahertzů. Pro zobrazení těchto vysokofrekvenčních signálů musí být šířka pásma osciloskopu alespoň 500 MHz. Tak široká skupina opravdu „rozšiřuje“ cenu osciloskopu.

Příkladem je digitální osciloskop U1610A, který není zobrazen na obrázku 5. Jeho šířka pásma je 100 MHz a cena je téměř 200 000 rublů. Souhlasíte, že ne každý si může dovolit koupit takové drahé zařízení.

Obrázek 5

Nechte čtenáře, aby tento obrázek nepovažoval za reklamu, protože všechny souřadnice prodávajícího nejsou překresleny: na místě tohoto obrázku se může objevit jakýkoli podobný snímek obrazovky.

Typy studovaných signálů a jejich parametry

Nejběžnějším typem oscilace v přírodě a technologii je sinusoid. Toto je stejná dlouho trpící funkce Y = sinX, která se ve škole konala v hodinách trigonometrie. Docela mnoho elektrických a mechanických procesů má sinusový tvar, i když v elektronické technologii se často používají i jiné formy signálů. Některé z nich jsou znázorněny na obrázku 6.

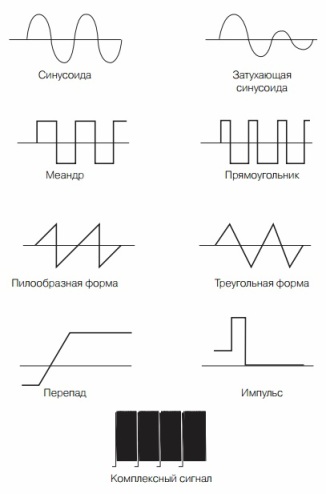
Obrázek 6. Formy elektrických vibrací

Periodické signály. Charakteristiky signálu

Univerzální elektronický osciloskop umožňuje přesné studium periodických signálů. Pokud na vstup Y odešlete skutečný zvukový signál, například hudební fonogram, na obrazovce se zobrazí náhodně blikající shluky. Přirozeně je nemožné podrobně prozkoumat takový signál. V tomto případě pomůže použití digitálního paměťového osciloskopu, který vám umožní uložit průběh.

Oscilace znázorněné na obrázku 6 jsou periodické, opakují se po určité časové periodě T. To lze podrobněji rozebrat na obrázku 7.

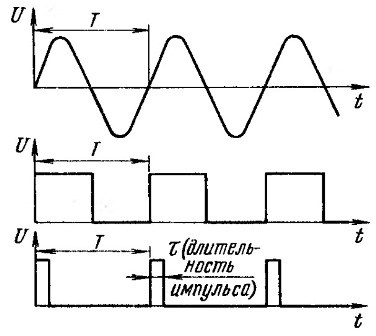
Obrázek 7. Periodické fluktuace

Oscilace jsou znázorněny v dvourozměrném souřadném systému: napětí je měřeno podél osy souřadnic a čas je měřen podél osy vodorovných os. Napětí se měří ve voltech, čas v sekundách. U elektrických vibrací je čas často měřen v milisekundách nebo mikrosekundách.

Kromě složek X a Y obsahuje průběh také složku Z - intenzitu, nebo jednoduše jas (obrázek 8). Je to ona, která zapne paprsek po dobu dopředného paprsku a zhasne po dobu zpětného zdvihu. Některé osciloskopy mají vstup pro řízení jasu, který se nazývá vstup Z. Pokud na tento vstup aplikujete pulzní napětí z příkladného generátoru, můžete na obrazovce vidět frekvenční štítky. To vám umožní přesněji změřit délku signálu podél osy X.

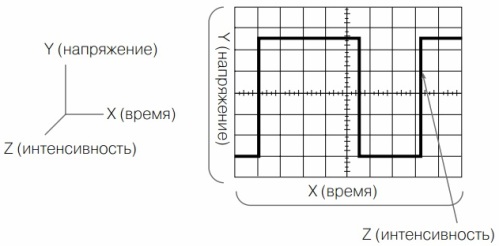
Obrázek 8. Tři složky zkoumaného signálu

Moderní osciloskopy mají zpravidla časově kalibrované rozmítání, které umožňuje přesné načasování. Proto není použití externího generátoru k vytváření značek prakticky nutné.

Na vrcholu obrázku 7 je sinusová vlna. Je snadné vidět, že začíná na začátku souřadnicového systému. Během doby T (periody) se provede jedna úplná oscilace. Pak se vše opakuje, v dalším období. Takové signály se nazývají periodické.

Obdélníkové signály jsou zobrazeny pod sinusovou vlnou: meandr a pravoúhlý puls. Jsou také periodické s periodou T. Doba trvání pulsu je označena jako τ (tau). V případě meandru je doba trvání pulzu τ stejná jako doba pauzy mezi impulsy, jen polovina periody T. Proto je meandr zvláštním případem obdélníkového signálu.

Clo a sazba cla

Pro charakterizaci pravoúhlých pulzů se používá parametr zvaný pracovní cyklus. Toto je poměr periody opakování T impulsu k trvání pulsu τ. Pro meandr je pracovní cyklus roven dvěma, - hodnota je bezrozměrná: S = T / τ.

V anglické terminologii je pravý opak. Zde jsou pulzy charakterizovány pracovním cyklem, poměrem doby trvání pulsu k periodě pracovního cyklu: D = τ / T. Faktor výplně je vyjádřen v %%. Tudíž pro meandr D = 50%. Ukazuje se, že D = 1 / S, pracovní cyklus a pracovní cyklus jsou vzájemně inverzní, ačkoli charakterizují stejný parametr pulsu. Tvar vlny meandru je znázorněn na obrázku 9.

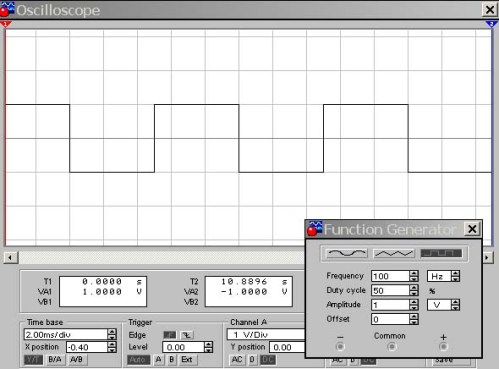
Obrázek 9. Vlnová křivka meandru D = 50%

Zde je vstup osciloskopu připojen k výstupu funkčního generátoru, který je zobrazen okamžitě ve spodním rohu obrázku. A zde může pozorný čtenář položit otázku: „Amplituda výstupního signálu z 1V generátoru, citlivost vstupu osciloskopu je 1V / div. A na obrazovce se zobrazují obdélníkové impulsy s velikostí 2V. Proč?

Skutečnost je taková, že funkční generátor generuje bipolární pravoúhlé impulzy vzhledem k hladině 0V, přibližně stejné jako sinusoid, s pozitivními a negativními amplitudami. Proto jsou na obrazovce osciloskopu pozorovány impulsy s rozpětím ± 1V. Na následujícím obrázku změníme pracovní cyklus, například, na 10%.

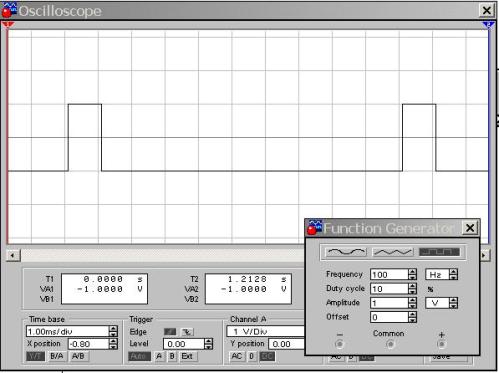
Obrázek 10. Obdélníkový moment D = 10%

Je snadné vidět, že perioda opakování pulsu je 10 buněk, zatímco doba trvání pulsu je pouze jedna buňka. Proto D = 1/10 = 0,1 nebo 10%, jak je vidět z nastavení generátoru. Pokud použijete vzorec pro výpočet pracovního cyklu, dostanete S = T / τ = 10/1 = 1 - hodnota je bezrozměrná. Zde můžeme dojít k závěru, že pracovní cyklus charakterizuje impuls mnohem jasněji než pracovní cyklus.

Ve skutečnosti samotný signál zůstal stejný jako na obrázku 9: pravoúhlý puls s amplitudou 1 V a frekvencí 100 Hz. Mění se pouze faktor plnění nebo pracovní cyklus, vypadá to, že je někdo známější a pohodlnější. Ale pro pohodlí pozorování na obrázku 10 je doba skenování na polovinu ve srovnání s obrázkem 9 a je 1ms / div. Doba signálu tedy na obrazovce zabere 10 buněk, což značně usnadňuje ověření, že pracovní cyklus je 10%. Při použití skutečného osciloskopu je doba trvání rozmítání vybrána přibližně stejně.

Měření pravoúhlého pulzního napětí

Jak je uvedeno na začátku článku, osciloskop měří napětí, tj. potenciální rozdíl mezi dvěma body. Obvykle se měření provádí ve vztahu ke společnému vodiči, kostře (nulové volty), ačkoli to není nutné. V zásadě je možné měřit od minimálních po maximální hodnoty signálu (špičková hodnota, vrchol-vrchol). V každém případě jsou kroky měření poměrně jednoduché.

Obdélníkové impulsy jsou nejčastěji unipolární, což je typické pro digitální technologii. Jak měřit napětí pravoúhlého pulsu je znázorněno na obrázku 11.

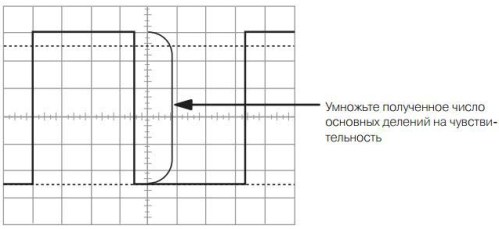
Obrázek 11. Měření amplitudy pravoúhlého pulsu

Pokud je citlivost kanálu pro vertikální odchylku 1 V / div, pak se ukáže, že obrázek ukazuje puls s napětím 5,5 V. S citlivostí 0,1 V / div. Napětí bude pouze 0,5V, i když na obrazovce oba impulsy vypadají přesně stejně.

Co jiného lze vidět v pravoúhlém impulsu

Obdélníkové impulsy znázorněné na obrázcích 9, 10 jsou jednoduše ideální, protože jsou syntetizovány společností Electronics WorkBench. Frekvence pulzů je pouze 100 Hz, proto nemohou nastat problémy s „pravoúhlostí“ obrazu. Ve skutečném zařízení, při vysoké opakovací frekvenci, jsou impulsy poněkud zkreslené, v první řadě se objevují různé rázy a impulzy způsobené instalační indukčností, jak je znázorněno na obrázku 12.

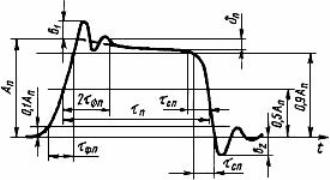
Obrázek 12. Skutečný obdélníkový impuls

Pokud těmto „maličkostem“ nevěnujete pozornost, vypadá pravoúhlý impuls jako na obrázku 13.

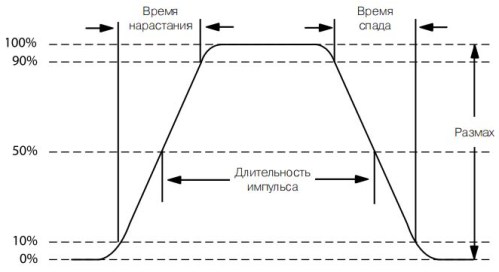
Obrázek 13. Parametry obdélníkového pulsu

Obrázek ukazuje, že náběžné a zadní okraje pulsu se neobjeví okamžitě, ale mají určité doby náběhu a pádu a jsou poněkud nakloněné vzhledem ke svislé linii. Tento sklon je způsoben kmitočtovými vlastnostmi mikroobvodů a tranzistorů: čím vyšší je frekvenční tranzistor, tím méně „front“ pulzů. Trvání pulsu je proto určeno hladinou 50% celého rozsahu.

Ze stejného důvodu je amplituda impulsu určena úrovní 10 ... 90%. Trvání impulsu, stejně jako napětí, je určeno vynásobením počtu dělení horizontální stupnice hodnotou dělení, jak je znázorněno na obrázku 14.

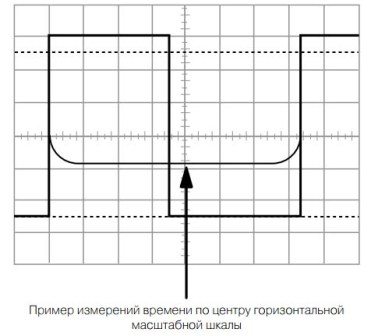
Obrázek 14.

Obrázek ukazuje jednu periodu obdélníkového pulzu, mírně odlišnou od meandru: doba trvání pozitivního pulzu je 3,5 divize horizontální stupnice a doba pauzy je 3,8 divize. Doba opakování pulsu je 7,3 divizí. Takový obrázek může patřit k několika různým impulzům s různými frekvencemi. Vše bude záviset na délce rozmítání.

Předpokládejme trvání skenování 1ms / div. Pak je perioda opakování pulzu 7,3 * 1 = 7,3 ms, což odpovídá frekvenci F = 1 / T = 1 / 7,3 = 0,1428 KHz nebo 143 Hz. Pokud je doba trvání skenování 1 µs / div, pak se frekvence ukáže tisíckrát vyšší, a to 143KHZ.

Použitím dat na obrázku 14 není obtížné vypočítat pracovní cyklus pulsu: S = T / τ = 7,3 / 3,5 = 2,0857, ukazuje se téměř jako meandr. Pracovní cyklus pracovního cyklu D = τ / T = 3,5 / 7,3 = 0,499 nebo 47,9%. Je třeba poznamenat, že tyto parametry v žádném případě nezávisí na frekvenci: pracovní cyklus a pracovní cyklus byly vypočteny jednoduše dělením na tvaru vlny.

S obdélníkovými impulsy se vše zdá být jasné a jednoduché. Ale na sinusovou vlnu jsme úplně zapomněli. Ve skutečnosti je to stejné: můžete měřit napětí a časové parametry. Jedna periody sinusové vlny je znázorněna na obrázku 15.

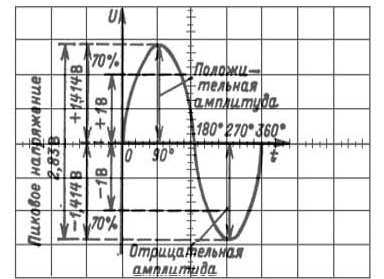
Obrázek 15. Parametry sinusové vlny

Je zřejmé, že pro sinusoidy znázorněné na obrázku je citlivost vertikálního vychylovacího kanálu 0,5 V / div. Zbývající parametry lze snadno určit vynásobením počtu dělení 0,5 V / div.

Sinusová vlna může být další, která bude muset být měřena s citlivostí, například 5V / div. Pak místo 1V získáte 10V. Na obrazovce však obraz obou sinusoidů vypadá úplně stejně.

Načasování zobrazeného sinusoidu není známo. Pokud předpokládáme, že doba trvání skenování je 5ms / div, bude perioda 20ms, což odpovídá frekvenci 50 Hz. Čísla ve stupních na časové ose označují fázi sinusoidy, ačkoli to není zvlášť důležité pro jeden sinusoid. Častěji je nutné stanovit fázový posun (přímo v milisekundách nebo mikrosekundách) alespoň mezi dvěma signály. To se nejlépe provede pomocí dvou paprskového osciloskopu. Jak se to dělá, bude ukázáno níže.

Jak měřit proud pomocí osciloskopu

V některých případech je nutné měřit velikost a tvar proudu. Například střídavý proud protékající kondenzátorem je před napětím o ¼ periody. Poté je do otevřeného obvodu zahrnut odpor s malým odporem (desetiny Ohmu). Takový odpor nemá vliv na provoz obvodu. Úbytek napětí na tomto odporu bude zobrazovat tvar a velikost proudu protékajícího kondenzátorem.

Obdobný kalibrační ampérmetr je uspořádán přibližně stejným způsobem, který bude zahrnut do přerušení elektrického obvodu. V tomto případě je měřicí odpor umístěn uvnitř samotného ampérmetru.

Obvod pro měření proudu kondenzátorem je znázorněn na obrázku 16.

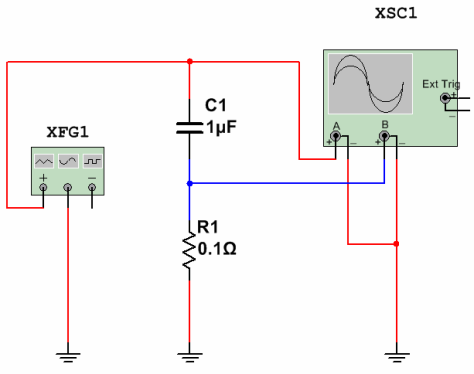
Obrázek 16. Měření proudu pomocí kondenzátoru

Sinusové napětí 50 Hz s amplitudou 220 V z generátoru XFG1 (červený paprsek na obrazovce osciloskopu) je přiváděn do sériového obvodu z kondenzátoru C1 a měřicího odporu R1. Úbytek napětí na tomto odporu ukáže tvar, fázi a velikost proudu přes kondenzátor (modrý paprsek). Jak to bude vypadat na obrazovce osciloskopu je znázorněno na obrázku 17.

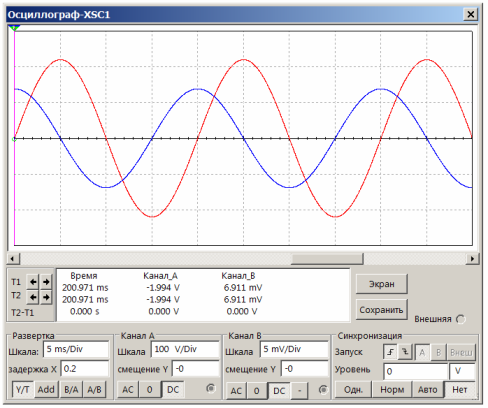
Obrázek 17. Proud přes kondenzátor je o ahead periodu před napětím

Při frekvenci sinusové vlny 50 Hz a době skenování 5 ms / Div trvá jedna periody sinusové vlny 4 dělení podél osy X, což je velmi výhodné pro pozorování. Je snadné vidět, že modrý paprsek je před červenou o přesně 1 dělení podél osy X, což odpovídá periodě ¼. Jinými slovy, proud přes kondenzátor je před fázovým napětím, což je plně v souladu s teorií.

Pro výpočet proudu přes kondenzátor stačí použít Ohmův zákon: I = U / R. Pokud je odpor měřicího odporu 0,1 Ohm, pokles napětí na něm je 7 mV. Toto je hodnota amplitudy. Maximální proud procházející kondenzátorem bude 7 / 0,1 = 70 mA.

Měření tvaru proudu kondenzátorem není žádný velmi naléhavý úkol, vše je jasné a bez měření. Místo kondenzátoru může být jakékoli zatížení: induktor, motorové vinutí, tranzistorový zesilovač a mnohem více. Je důležité, aby tuto metodu bylo možné použít ke studiu proudu, který se v některých případech výrazně liší formou od napětí.

Boris Aladyshkin