"ทุกอย่างไหล" หรือกฎของโอห์มสำหรับคนที่อยากรู้อยากเห็น

แม้แต่คนขี้เกียจคนสุดท้ายที่เรียนมาสักพักหนึ่งในเกรด 10 จะบอกครูว่า กฎของโอห์ม - นี่คือ“ U เท่ากับฉันคูณ R” น่าเสียดายที่นักเรียนที่เก่งที่สุดจะพูดน้อยมาก - ด้านกายภาพของกฎของโอห์มจะยังคงเป็นปริศนาสำหรับเขาถึงแมวน้ำเจ็ดดวง ฉันอนุญาตให้ตัวเองแบ่งปันกับเพื่อนร่วมงานของฉันประสบการณ์ของฉันในการนำเสนอหัวข้อดั้งเดิมนี้ดูเหมือน

เป้าหมายของกิจกรรมการสอนของฉันคือวิชาศิลปะและมนุษยธรรมชั้น 10 ซึ่งมีความสนใจหลักตามที่ผู้อ่านคาดเดาอยู่ไกลจากฟิสิกส์ นั่นคือเหตุผลที่การสอนวิชานี้ได้รับความไว้วางใจจากผู้เขียนในสายงานนี้ซึ่งโดยทั่วไปแล้วสอนวิชาชีววิทยา ไม่กี่ปีที่ผ่านมา

บทเรียนเกี่ยวกับกฎของโอห์มเริ่มต้นด้วยข้อความที่ไม่สำคัญว่ากระแสไฟฟ้าคือการเคลื่อนที่ของอนุภาคที่มีประจุในสนามไฟฟ้า หากเพียงแรงไฟฟ้ากระทำกับอนุภาคที่มีประจุอนุภาคนั้นก็จะเร่งตามกฎข้อที่สองของนิวตัน และถ้าเวกเตอร์ของแรงไฟฟ้าที่กระทำกับอนุภาคที่มีประจุนั้นคงที่ในวิถีทั้งหมดมันก็จะถูกเร่งอย่างเท่าเทียมกัน เหมือนน้ำหนักตกอยู่ภายใต้อิทธิพลของแรงโน้มถ่วง

แต่ที่นี่พลร่มตกลงอย่างผิดปกติ หากเราละเลยลมอัตราการตกจึงเป็นค่าคงที่ แม้แต่นักเรียนด้านศิลปะและมนุษยธรรมก็จะตอบว่านอกเหนือจากแรงดึงดูดของโลกแรงโน้มถ่วงอีกอันยังทำหน้าที่แทนร่มชูชีพ - พลังแห่งแรงต้านอากาศ แรงนี้มีค่าเท่ากันกับแรงดึงดูดของร่มชูชีพจากโลกและอยู่ในทิศทางตรงกันข้าม ทำไม? นี่คือคำถามสำคัญของบทเรียน หลังจากการสนทนาเราสรุปได้ว่าแรงลากเพิ่มขึ้นเมื่ออัตราการตกเพิ่มขึ้น ดังนั้นร่างกายที่ตกลงมาจะเร่งความเร็วที่แรงโน้มถ่วงและความต้านทานอากาศจะเท่ากันและร่างกายก็จะลดลงด้วยความเร็วคงที่

จริงในกรณีของพลร่มสถานการณ์ค่อนข้างซับซ้อน ร่มชูชีพไม่เปิดทันทีและพลร่มชูชีพเร่งความเร็วสูงขึ้นอย่างมีนัยสำคัญ และเมื่อร่มชูชีพได้เปิดไปแล้วการตกเริ่มต้นด้วยการชะลอตัวซึ่งจะดำเนินต่อไปจนกว่าแรงโน้มถ่วงและแรงต้านของอากาศจะสมดุลกัน

สำหรับการบรรทุกสินค้าที่มีร่มชูชีพที่มีมวลรวมลดลงอย่างรวดเร็ว โวลต์เราสามารถเขียน: mg - F (โวลต์) = 0 โดยที่ F (โวลต์) เป็นแรงต้านอากาศซึ่งถือว่าเป็นหน้าที่ของอัตราการตก เกี่ยวกับรูปแบบของฟังก์ชั่น F (โวลต์) เราสามารถพูดได้เพียงสิ่งเดียวเท่านั้น: มันกำลังเติบโตอย่างน่าเบื่อ เป็นกรณีนี้ที่ให้ความเร็วคงที่

ในกรณีที่ง่ายที่สุดเมื่อ F (โวลต์) = k ความเร็วคงที่ซึ่งร่มชูชีพจะตกจะเท่ากับ mg / k เรามาแปลงกันตอนนี้ ให้ร่มชูชีพตกจากที่สูง จากนั้นความแตกต่างของพลังงานศักย์ของร่างกายก่อนและหลังการล่มสลายจะเท่ากับ mgh = mU โดยที่ U คือพลังงานศักย์ของมวลร่างกายหน่วยที่ความสูง h หรือความต่างศักย์ของสนามโน้มถ่วงที่จุดเริ่มต้นและจุดสุดท้ายของอุบัติการณ์

ในมุมมองของที่กล่าวมาเราได้รับสูตร: F (โวลต์) = mU / h (1)

และกลับไปที่ตัวนำผ่านที่กระแสไฟฟ้าไหล อนุภาคที่มีประจุจำนวนมากเคลื่อนที่ไปตามตัวนำซึ่งชนกับอะตอมบ่อยกว่าที่พวกมันบินเร็วขึ้น การเปรียบเทียบกับการสืบเชื้อสายของร่มชูชีพค่อนข้างโปร่งใสความแตกต่างเพียงอย่างเดียวคือมี“ ร่มชูชีพ” จำนวนมากและพวกมันเคลื่อนไหวไม่ได้อยู่ในแรงโน้มถ่วง แต่อยู่ในสนามไฟฟ้า เนื่องจากสถานการณ์เหล่านี้ (1) สามารถเขียนใหม่ในรูปแบบ: F (โวลต์) = eU / l, (2)

เมื่อ e คือประจุอนุภาค U คือความต่างศักย์ไฟฟ้าที่ปลายตัวนำตัวนำ l คือความยาวของตัวนำความแรงของกระแสเท่ากับ I = neS โดยที่ n คือจำนวนอนุภาคที่มีประจุต่อปริมาตรหน่วย S คือพื้นที่หน้าตัดของตัวนำเป็นความเร็วของอนุภาค (เพื่อความง่าย

ในการรับการพึ่งพา I (U) คุณจำเป็นต้องรู้การพึ่งพา F () อย่างชัดเจน ตัวเลือกที่ง่ายที่สุด (F = k) จะให้กฎของโอห์มทันที (I ~ U):

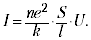
ค่านี้เรียกว่าค่าการนำไฟฟ้าและส่วนกลับซึ่งเรียกว่าความต้านทาน เพื่อเป็นเกียรติแก่ผู้ค้นพบของกฎหมายความต้านทานมักจะแสดงออกเป็นโอห์ม

ค่า (ne2 / k) เรียกว่าค่าการนำไฟฟ้าจำเพาะและค่าผกผันของมันเรียกว่าค่าความต้านทานจำเพาะ ค่าเหล่านี้เป็นลักษณะของวัสดุที่ตัวนำประกอบด้วย เป็นสิ่งสำคัญที่ค่าการนำไฟฟ้าเป็นสัดส่วนกับจำนวนของอนุภาคที่มีประจุต่อหน่วยปริมาตร (n) ในโลหะและสารละลายอิเล็กโทรไลต์จำนวนนี้มีขนาดใหญ่ แต่ในไดอิเล็กทริกจะมีขนาดเล็ก จำนวนของอนุภาคที่มีประจุต่อปริมาตรต่อหน่วยของก๊าซสามารถขึ้นอยู่กับสนามที่ใช้ (เช่นเป็นฟังก์ชันของ U) ดังนั้นกฎของโอห์มจึงไม่สามารถใช้กับก๊าซได้

ในการได้มาซึ่งกฎของโอห์มเราได้ตั้งสมมติฐานหนึ่งที่ไม่ชัดเจน เรายอมรับว่าแรงที่ยับยั้งการเคลื่อนที่ของอนุภาคที่มีประจุนั้นแปรผันตามความเร็วของมัน แน่นอนว่าใคร ๆ ก็สามารถลองพิสูจน์ความคิดนี้ได้บ้าง แต่การตรวจสอบการทดลองดูเหมือนจะน่าเชื่อถือมากขึ้น

การยืนยันการทดลองของสมมติฐานนี้เป็นที่ชัดเจนว่าเป็นการตรวจสอบกฎหมายของโอห์มเองเช่น สัดส่วนของ U และ I ดูเหมือนว่านี่ไม่ใช่เรื่องยากที่จะทำ: เรามีโวลต์มิเตอร์และแอมป์มิเตอร์! อนิจจาทุกอย่างไม่ง่ายเลย เราต้องอธิบายให้นักเรียนของเราฟังว่าโวลต์มิเตอร์เหมือนแอมมิเตอร์วัดไม่ได้เป็นแรงดัน แต่มีความแข็งแรงในปัจจุบัน และเรามีสิทธิ์ในการตั้งค่าโวลต์ในระดับโวลต์มิเตอร์เท่านั้นเพราะในตอนแรกเรารู้กฎของโอห์มซึ่งเราต้องการตรวจสอบ ต้องการแนวทางอื่น

ตัวอย่างเช่นคุณสามารถใช้แนวคิดต่อไปนี้ เราเชื่อมต่อแบตเตอรี่ n ก้อนเป็นอนุกรมและสมมติว่าแรงดันไฟฟ้าในกรณีนี้เพิ่มขึ้น n เท่า หากกฎของโอห์มเป็นจริงความแข็งแกร่งในปัจจุบันก็จะเพิ่มขึ้น n เท่าด้วยซึ่งอัตราส่วนที่ n / I (n) จะไม่ขึ้นอยู่กับ n สมมติฐานนี้เป็นธรรมจากประสบการณ์ จริงแบตเตอรี่ยังมีความต้านทานภายในซึ่งเป็นสาเหตุที่ค่าของ n / I (n) เติบโตอย่างช้าๆเมื่อเพิ่ม n แต่ก็ไม่ยากที่จะแก้ไข (G. Ohm เองวัดความเครียดในวิธีที่ต่างกันซึ่งนักเรียนสามารถอ่านได้ในตำราของ G.Ya. Myakishev และคนอื่น ๆ )

เราถามคำถาม:““ ในกลุ่มดาวเตียวเซติระยะไกล” ไม่ใช่กฎของโอห์ม แต่เป็นกฎของนักวิชาการท้องถิ่นนักวิชาการเอก X ตามกฎของ X ความแข็งแรงในปัจจุบันเป็นสัดส่วนกับกำลังสองของความต่างศักย์ที่ปลายตัวนำ แรงเบรกของอนุภาคขึ้นอยู่กับความเร็วของพวกเขาใน Tau Ceti อย่างไร” ด้วยความช่วยเหลือของการแปลงแบบง่าย ๆ นักเรียนจะได้ข้อสรุปว่าแรงเป็นสัดส่วนกับสแควร์รูทของความเร็ว

และตอนนี้เราจะไปสู่กระบวนการอื่น: การเคลื่อนที่ของน้ำในท่อที่ปลายสุดของแรงกดดันที่แตกต่างกัน ที่นี่เรามีสถานการณ์ที่แตกต่างอย่างสิ้นเชิง: ไม่แยกอนุภาคที่เคลื่อนที่ถูกับวัสดุที่อยู่กับที่ตลอดทั้งตัวนำ แต่ชั้นของอนุภาคเคลื่อนที่ถูกับซึ่งกันและกัน และสถานการณ์เช่นนี้เป็นการเปลี่ยนแปลงเหตุผลทางกายภาพทั้งหมด

แรงสองแรงกระทำบนชั้นของน้ำที่เคลื่อนที่ในท่อ:

a) ความแตกต่างของแรงกดที่ปลายสุดของชั้น;

b) แรงเสียดทานต่อชั้นน้ำที่อยู่ใกล้เคียง

หากความเร็วคงที่ของเลเยอร์ถูกสร้างขึ้นแรงเหล่านี้จะเท่ากันและไปในทิศทางตรงกันข้าม

แรงเสียดทานต่อชั้นน้ำที่อยู่ใกล้เคียงสามารถทำให้การเคลื่อนที่ช้าลงหากว่าชั้นน้ำที่แตกต่างกันเคลื่อนที่ด้วยความเร็วที่ต่างกัน ในตัวนำตัวนำความเร็วของอนุภาคที่มีประจุไม่ได้ขึ้นอยู่กับว่าอยู่ที่ขอบตัวนำหรืออยู่ตรงกลาง แต่น้ำที่อยู่ตรงกลางของท่อเคลื่อนที่อย่างรวดเร็วและช้าไปตามขอบบนพื้นผิวของท่อความเร็วน้ำนั้นเป็นศูนย์

อะนาล็อกของความแข็งแรงในปัจจุบันถือได้ว่าเป็นการไหลของน้ำเช่น ปริมาณน้ำที่ไหลออกจากท่อต่อหน่วยเวลา เนื่องจากความเร็วของน้ำในชั้นต่าง ๆ ไม่เท่ากันการคำนวณอัตราการไหลจึงไม่ง่ายนักความแตกต่างของศักย์ไฟฟ้าแบบอะนาล็อกคือความแตกต่างของความดันที่ปลายท่อ

เช่นเดียวกับในตัวนำที่มีกระแสไฟฟ้าพบสัดส่วนโดยตรงในท่อที่มีน้ำระหว่างความแตกต่างของความดันที่ปลายและอัตราการไหล แต่สัมประสิทธิ์ของสัดส่วนต่างกันโดยสิ้นเชิง ประการแรกอัตราการไหลของน้ำไม่เพียง แต่ขึ้นอยู่กับพื้นที่หน้าตัดของท่อเท่านั้น แต่ยังรวมถึงรูปร่างด้วย หากท่อมีรูปทรงกระบอกอัตราการไหลจะเป็นสัดส่วนโดยตรงไม่ใช่พื้นที่หน้าตัด แต่เป็นรูปสี่เหลี่ยมจัตุรัส การพึ่งพาอาศัยกันนี้เรียกว่ากฎหมาย Poiseuille

นี่เป็นเวลาที่จะระลึกถึงวิชากายวิภาคศาสตร์สรีรวิทยาและสุขอนามัยที่เรียนในเกรด 9 ร่างกายมนุษย์มีเส้นเลือดจำนวนมากเชื่อมต่อกัน สมมติว่าหนึ่งในเรือเหล่านี้ขยายและรัศมีของมันเพิ่มขึ้นเล็กน้อยเพียงสองครั้ง ปริมาณของเลือดที่ไหลผ่านจะเพิ่มขึ้นด้วยความดันเท่ากันที่ปลายเรือ พื้นที่หน้าตัดเป็นสัดส่วนกับกำลังสองของรัศมีและพื้นที่ของพื้นที่หน้าตัดเป็นสัดส่วนกับรัศมีสี่องศา ดังนั้นเมื่อรัศมีเพิ่มเป็นสองเท่าการไหลเวียนของเลือดจะเพิ่มขึ้น 16 (!) เท่า นั่นคือพลังของกฎหมาย Poiseuille ซึ่งอนุญาตให้สร้างกลไกที่มีประสิทธิภาพมากสำหรับการแจกจ่ายเลือดระหว่างอวัยวะต่าง ๆ หากอิเล็กตรอนไม่ได้ไหลผ่านหลอดเลือด แต่การไหลของพวกเขาจะเพิ่มขึ้นเพียงสี่ครั้ง

คำอธิบายของหัวข้อที่อธิบายข้างต้นแตกต่างจากแบบดั้งเดิม ประการแรกมีการใช้บทเรียนสามบทในหัวข้อซึ่งด้วยการขาดแคลนชั่วโมงปัจจุบันถือได้ว่าเป็นความหรูหราที่ไม่อาจยอมรับได้สำหรับวิทยาศาสตร์ธรรมชาติ อย่างไรก็ตามนี่เป็นความจริงโดยข้อเท็จจริงที่ว่ามันเป็นไปได้ที่จะเปิดเผยความหมายทางกายภาพของกฎหมายและทำให้นักเรียนมีวิธีการที่พวกเขาสามารถใช้ในการวิเคราะห์กระบวนการทางกายภาพที่หลากหลาย: การล่มสลายของร่างกายในอากาศ, การเคลื่อนที่ของของเหลวในท่อ ในการวิเคราะห์ทางเดินของกระแสไฟฟ้าผ่านสุญญากาศและผ่านแก๊ส

วิธีนี้เรียกว่าการบูรณาการแบบสหวิทยาการ ด้วยความช่วยเหลือเราได้แสดงให้นักเรียนเห็นคุณสมบัติทั่วไปในระยะไกลในส่วนแรกของฟิสิกส์เราแสดงให้เห็นว่าฟิสิกส์ไม่ใช่ "พวง" ของ "กฎทางกายภาพ" ที่ไม่ได้เชื่อมต่อซึ่งกันและกัน แต่เป็นอาคารที่เรียว แน่นอนว่าเป็นเรื่องจริงสำหรับสาขาวิชาวิทยาศาสตร์อื่น ๆ และดูเหมือนว่าการเสียชั่วโมงฝึกอบรมอย่างไม่มีเหตุผลจะได้ผลอย่างเต็มที่

อ่านเพิ่มเติม:วิธีใช้มัลติมิเตอร์