Каква е връзката между телените участъци и заешката популация?

През 1202 г. италианският математик Леонардо Фибоначи публикува работата си под заглавието „Книга на абакуса“ („Книга на изчисленията“), в която също описва числови серии, увековечени от неговото име. В една от главите Фибоначи се опитва математически да покаже как ще се увеличи броят на зайците. Той счита следните условия за условия:

1) първите два месеца чифт зайци не дава потомство;

2) започвайки от третия месец, чифт зайци дава още една двойка зайци.

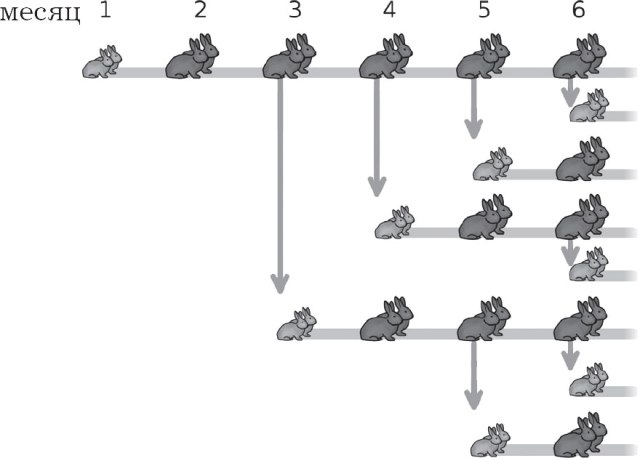
В резултат на изграждането на модел на растеж на популацията на зайци получаваме следната серия от числа, отбелязвайки увеличаването на броя на зайците всеки месец:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 …

1 + 1 = 2; 1 + 2 = 3; 2 + 3 = 5; 3 + 5 = 8…

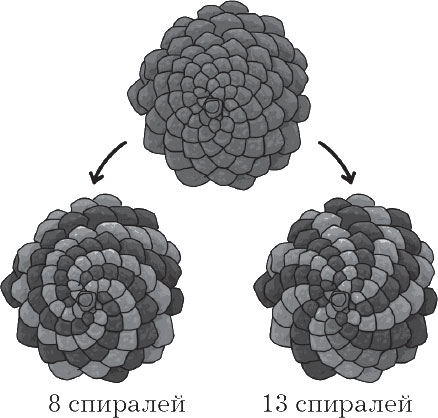
Ако внимателно погледнете подутина, ще видите, че повърхността му се състои от люспи, които са усукани в спирала в съответствие с последователността на Фибоначи. Докато са в ананас или в цвете на слънчоглед, те са видими с просто око.

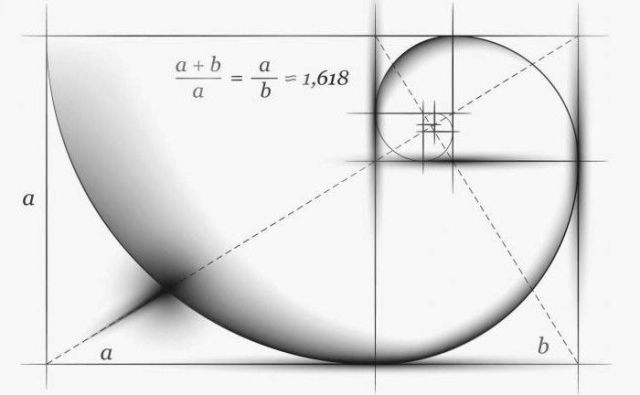
От времето на Античността на Златното съотношение числото = 1.618. Древните гърци считали стойността на идеалната пропорция. Златното съотношение е съотношението на всяко следващо число от серията на Фибоначи към предходното:

144/89=89/55=55/34=34/21=21/13=13/8=8/5=5/3=1,618...

Древните гърци са го използвали в архитектурата. Фасадата на Партенона в Атина има много сходни пропорции с правоъгълник, изграден на принципа на златното съотношение.

И така, каква е красотата на последователността на телените секции, номиналните токове на електрическите и прекъсващите токове на прекъсвачите? Изградете серия от числа със следните стойности: 1,5; 2.5; 4; 6; 10; 16; 25; 40; 63...

Номинални токове на електромагнитни стартери:

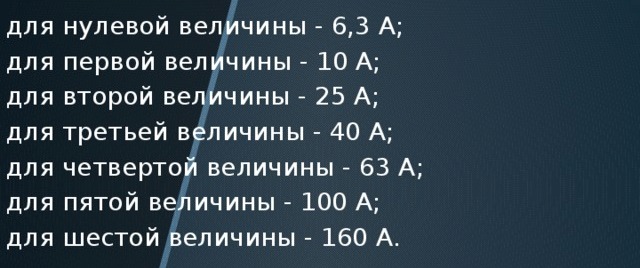
Така че, ако разделите 2,5 / 1,5; 4 / 2.5; 6.3 / 4; 10 / 6.3; 16/10; 25/16; 40/25; 63/40тогава получаваме около 1.6. Което съответства на правилото за златното съотношение. И отразява красотата и гениалността на природата дори в нашите скучни инженерни системи.

Какво мислиш? Това злополука ли е?

Въз основа на книгата "Страхотен роман за математиката. История на света през призмата на математиката" на Майкъл Лойн. Благодаря за препоръката от Владимир Кисел.

Алексей Бушняга