"Viss plūst" jeb Ohma likums ziņkārīgajiem

Pat pēdējais koferis, kādu laiku mācījies 10. klasē, skolotājam to pateiks Ohmas likums - tas ir “U ir vienāds ar I reizes R”. Diemžēl gudrākais izcilais students pateiks nedaudz vairāk - Ohmas likuma fiziskā puse viņam paliks noslēpums septiņiem zīmogiem. Es ļauju sev dalīties ar kolēģiem savā pieredzē, iepazīstinot ar šo šķietami primitīvo tēmu.

Manas pedagoģiskās darbības objekts bija mākslas un humanitārā 10. klase, kuras galvenās intereses, kā lasītājs domā, atrodas ļoti tālu no fizikas. Tāpēc šī priekšmeta mācīšana tika uzticēta šo rindu autoram, kurš, vispārīgi runājot, māca bioloģiju. Tas bija pirms dažiem gadiem.

Nodarbība par Ohmas likumu sākas ar triviālu paziņojumu, ka elektriskā strāva ir uzlādētu daļiņu kustība elektriskajā laukā. Ja uz uzlādētu daļiņu iedarbojas tikai elektrisks spēks, tad daļiņa paātrināsies saskaņā ar Ņūtona otro likumu. Un, ja elektriskā spēka vektors, kas iedarbojas uz uzlādēto daļiņu, ir nemainīgs visā trajektorijā, tad tas tiek vienādi paātrināts. Gluži tāpat kā svars nonāk gravitācijas ietekmē.

Bet šeit izpletņlēcējs nokrīt pilnīgi nepareizi. Ja vēju atstājam novārtā, tad tā krišanas ātrums ir nemainīgs. Pat mākslas un humanitārās klases students atbildēs, ka papildus gravitācijas spēkam uz krītošo izpletni iedarbojas vēl viens krītošs spēks - gaisa pretestības spēks. Šis spēks absolūtā vērtībā ir vienāds ar Zemes izpletņa pievilkšanas spēku un ir pretējs tam virzienā. Kāpēc? Tas ir galvenais stundas jautājums. Pēc nelielām diskusijām mēs secinām, ka vilces spēks palielinās, palielinoties krituma likmei. Tāpēc krītošais ķermenis paātrinās līdz ātrumam, ar kuru gravitācija un gaisa pretestība izlīdzinās, un ķermenis tālāk nokrīt ar nemainīgu ātrumu.

Tiesa, desantnieka gadījumā situācija ir nedaudz sarežģītāka. Izpletnis nekavējoties neatveras, un izpletņlēcējs paātrinās līdz ievērojami lielākam ātrumam. Un, kad izpletnis jau ir atvērts, kritiens sākas ar palēninājumu, kas turpinās līdz gravitācijas spēka un gaisa pretestības spēka līdzsvarošanai.

Izpletņa kravai ar kopējo masu m, kas nolaižas ar nemainīgu ātrumu v, mēs varam rakstīt: mg - F (v) = 0, kur F (v) Vai gaisa pretestības spēks tiek ņemts vērā kā kritiena ātruma funkcija. Attiecībā uz funkcijas F formu (v) līdz šim mēs varam pateikt tikai vienu lietu: tā pieaug vienmuļi. Tieši šis apstāklis ​​nodrošina ātruma stabilizāciju.

Vienkāršākā gadījumā, kad F (v) = k, nemainīgais ātrums, ar kādu izpletnis nokritīsies, būs vienāds ar mg / k. Tagad veiksim nelielu pārveidošanu. Izpletni ļaujiet nokrist no h augstuma. Tad ķermeņa potenciālo enerģiju starpība pirms un pēc kritiena būs vienāda ar mgh = mU, kur U ir masas vienības ķermeņa potenciālā enerģija augstumā h, vai gravitācijas lauka potenciālā starpība sākotnējā un beigu kritiena vietās.

Ņemot vērā iepriekš minēto, iegūstam formulu: F (v) = mU / h. (1)

Un tagad atpakaļ pie diriģenta, caur kuru plūst elektriskā strāva. Gar vadītāju pārvietojas liels skaits uzlādētu daļiņu, kuras biežāk saduras ar atomiem, jo ​​ātrāk tās lido. Analoģija ar izpletņa nolaišanos ir diezgan caurspīdīga, vienīgā atšķirība ir tā, ka ir daudz “izpletņu” un tie pārvietojas nevis gravitācijas, bet gan elektriskā lauka apstākļos. Ņemot vērā šos apstākļus (1), var pārrakstīt šādi: F (v) = eU / l, (2)

kur e ir daļiņu lādiņš, U ir elektriskā potenciāla starpība vadītāja galos, l ir vadītāja garums.Strāvas stiprums acīmredzami ir vienāds ar I = neS, kur n ir uzlādēto daļiņu skaits uz tilpuma vienību, S ir vadītāja šķērsgriezuma laukums, ir daļiņu ātrums (vienkāršības labad mēs pieņemam, ka visas uzlādētās daļiņas ir vienādas).

Lai iegūtu atkarību I (U), jums precīzi jāzina atkarība F (). Vienkāršākais variants (F = k) uzreiz dod Ohma likumu (I ~ U):

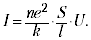
Vērtību sauc par vadītspēju, un tās abpusēju vērtību sauc par pretestību. Par godu likuma atklājējam pretestību parasti izsaka omi.

Vērtību (ne2 / k) sauc par īpatnējo vadītspēju, un tās apgriezto vērtību sauc par īpatnējo pretestību. Šīs vērtības raksturo diriģenta materiālu. Ir svarīgi, ka vadītspēja ir proporcionāla uzlādēto daļiņu skaitam tilpuma vienībā (n). Metālos un elektrolītu šķīdumos šis skaitlis ir liels, bet dielektrikā - mazs. Uzlādēto daļiņu skaits uz gāzes tilpuma vienību var būt atkarīgs no izmantotā lauka (t.i., tā ir U funkcija), tāpēc Ohmas likums neattiecas uz gāzēm.

Atvasinot Ohmas likumu, mēs izdarījām vienu acīmredzamu pieņēmumu. Mēs pieņēmām, ka lādētas daļiņas kustību kavējošais spēks ir proporcionāls tās ātrumam. Protams, varētu mēģināt kaut kā attaisnot šo ideju, taču eksperimentālā pārbaude izskatās daudz pārliecinošāka.

Šī pieņēmuma eksperimentāla pārbaude acīmredzami ir paša Ohmas likuma pārbaude, t.i. U un I proporcionalitāte Šķiet, ka to nav grūti izdarīt: mums ir voltmetrs un ampērmetrs! Diemžēl viss nav tik vienkārši. Mums studentiem jāpaskaidro, ka voltmetrs, tāpat kā ampērmetrs, mēra nevis spriegumu, bet strāvas stiprumu. Un mums ir tiesības iestatīt voltus uz voltmetra skalas tikai tāpēc, ka mēs sākotnēji zinām Ohmas likumu, kuru mēs vēlamies pārbaudīt. Nepieciešamas citas pieejas.

Varat, piemēram, izmantot šo ideju. Mēs savienojam n baterijas virknē un pieņemam, ka šajā gadījumā spriegums pieauga n reizes. Ja Ohmas likums ir taisnība, tad strāvas stiprums palielināsies arī n reizes, tāpēc attiecība n / I (n) nebūs atkarīga no n. Šis pieņēmums ir pamatots ar pieredzi. Tiesa, baterijām ir arī iekšējā pretestība, tāpēc n / I (n) vērtība lēnām aug, palielinoties n, taču to nav grūti izlabot. (Pats G. Ohms stresu mēra citādā veidā, par ko studenti var lasīt G. Ya. Mjakiševa un citu mācību grāmatā.)

Mēs uzdodam jautājumu: ““ Tālajā Tau Ceti zvaigznājā ”nav Ohmas likumi, bet gan lielā vietējā zinātnieka Akadēmiskā X likumi. Saskaņā ar X likumu strāvas stiprums ir proporcionāls potenciālās starpības kvadrātam diriģenta galos. Kā daļiņu bremzēšanas spēks ir atkarīgs no to ātruma uz Tau Ceti? ” Ar vienkāršu pārveidojumu palīdzību studenti secina, ka spēks ir proporcionāls ātruma kvadrātsaknei.

Un tagad pāriesim pie cita procesa: ūdens kustība caurulē, kuras galos tiek izveidoti dažādi spiedieni. Šeit mums ir pilnīgi atšķirīga situācija: nevis atsevišķas kustīgas daļiņas berzē pret nekustīgu materiālu, kas sadalīts pa visu diriģenta tilpumu, bet kustīgo daļiņu slāņi berzē viens pret otru. Un šis apstāklis ​​būtiski maina visu fizisko pamatojumu.

Divi spēki iedarbojas uz atsevišķu ūdens slāni, kas pārvietojas caurulē:

a) spiediena spēku atšķirība slāņa galos;

b) berzes spēks pret blakus esošajiem ūdens slāņiem.

Ja tiek noteikts nemainīgs slāņa ātrums, tad šie spēki ir vienādi un vērsti pretējos virzienos.

Berzes spēks pret blakus esošajiem ūdens slāņiem var palēnināt kustību tikai tad, ja dažādi ūdens slāņi pārvietojas ar dažādu ātrumu. Diriģentā uzlādēto daļiņu ātrums nav atkarīgs no tā, vai tās atrodas pie vadītāja malas vai tā centrā, bet ūdens caurules centrā ātri pārvietojas un lēnām gar malām, pašā caurules virsmā, ūdens ātrums ir nulle.

Strāvas stipruma analogu var uzskatīt par ūdens plūsmu, t.i. ūdens daudzums, kas izplūst no caurules laika vienībā. Tā kā ūdens ātrums dažādos slāņos nav vienāds, plūsmas ātruma aprēķināšana nav tik vienkārša.Elektrisko potenciālu atšķirības analogs ir spiediena starpība caurules galos.

Tāpat kā vadītājā ar strāvu, caurulē ar ūdeni tiek novērota tieša proporcionalitāte starp spiediena starpību galos un plūsmas ātrumu. Bet proporcionalitātes koeficients ir pilnīgi atšķirīgs. Pirmkārt, ūdens plūsmas ātrums ir atkarīgs ne tikai no caurules šķērsgriezuma laukuma, bet arī no tā formas. Ja caurule ir cilindriska, tad plūsmas ātrums ir tieši proporcionāls nevis šķērsgriezuma laukumam, bet gan tā kvadrātam (t.i., rādiusam līdz ceturtajai pakāpei). Šo atkarību sauc par Poiseuille likumu.

Šeit ir pienācis laiks atsaukt atmiņā anatomijas, fizioloģijas un higiēnas kursu, kas tika mācīts 9. klasē. Cilvēka ķermenī ir liels skaits kuģu, kas savienoti paralēli. Pieņemsim, ka viens no šiem kuģiem ir paplašinājies, un tā rādiuss ir nedaudz palielinājies, tikai divas reizes. Cik reizes ar tādu pašu spiedienu kuģa galos palielināsies asiņu daudzums, kas iet caur to? Šķērsgriezuma laukums ir proporcionāls rādiusa kvadrātam, un šķērsgriezuma laukuma kvadrāts ir proporcionāls ceturtās pakāpes rādiusam. Tāpēc, divreiz palielinot rādiusu, asins plūsma palielinās 16 (!) Reizes. Tāda ir Poiseuille likuma vara, kas ļauj izveidot ļoti efektīvu mehānismu asiņu pārdalei starp orgāniem. Ja elektroni neplūst caur asinsvadiem, bet to plūsma palielināsies tikai četras reizes.

Iepriekš aprakstītās tēmas apraksts atšķiras no tradicionālās. Pirmkārt, tēmai tiek veltītas trīs nodarbības, kuras, ņemot vērā pašreizējo stundu trūkumu, var uzskatīt par dabaszinātņu nepieļaujamu greznību. Tomēr tas tiek pamatots ar faktu, ka ir iespējams diezgan vienkārši un tautā atklāt fizisko likuma nozīmi un aprīkot studentus ar metodoloģiju, kuru viņi var izmantot, lai analizētu dažādus fiziskus procesus: ķermeņa krišanu gaisā, šķidruma kustību caurulē, uzlādētu daļiņu kustību gar vadītāju un vēlāk analizējot elektriskās strāvas caurlaidību caur vakuumu un caur gāzēm.

Šo pieeju sauc par starpdisciplināru integrāciju. Ar tās palīdzību mēs studentiem parādījām kopīgās iezīmes tālajos, no pirmā acu uzmetiena fizikas sadaļās, mēs parādījām, ka fizika nav “fizikālo likumu” “ķekars”, kas nav savstarpēji saistīti, bet gan tievs būve. Tas pats, protams, attiecas arī uz citām zinātnes disciplīnām. Un tā, šķiet, neracionāla mācību stundu izšķērdēšana pilnībā atmaksājas.

Lasīt arī:Kā izmantot multimetru