Jaké je spojení mezi částmi drátu a populací králíků?

V roce 1202 zveřejnil italský matematik Leonardo Fibonacci své dílo pod názvem „Kniha počítadla“ („Kniha výpočtů“), ve kterém také popsal číselné řady zvěčněné svým jménem. V jedné z kapitol se Fibonacci pokouší matematicky ukázat, jak se počet králíků zvýší. Za podmínky považoval následující hypotézy:

1) první dva měsíce pár králíků nedává potomstvo;

2) od třetího měsíce dává pár králíků další pár králíků.

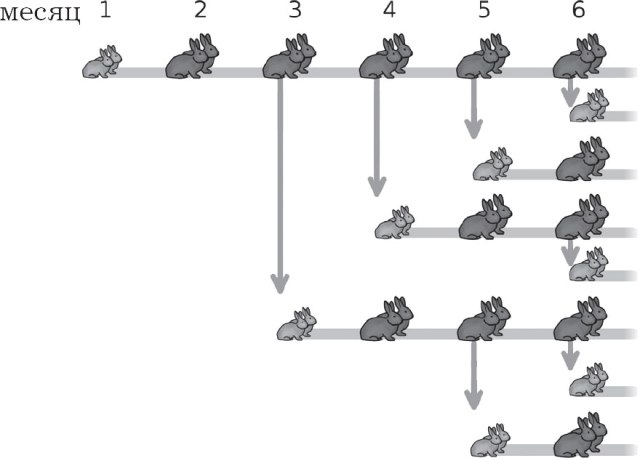
V důsledku konstrukce modelu růstu populace králíků získáme následující řadu čísel, přičemž každý měsíc zaznamenáváme nárůst počtu králíků:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144 …

1 + 1 = 2; 1 + 2 = 3; 2 + 3 = 5; 3 + 5 = 8…

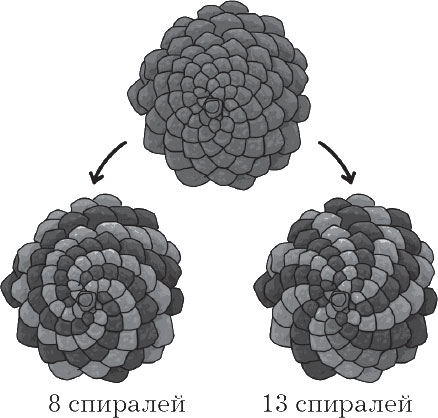
Pokud se pečlivě podíváte na ránu, uvidíte, že její povrch je tvořen šupinami, které jsou krouceny ve spirále v souladu s Fibonacciho sekvencí. Když jsou v ananasu nebo v květu slunečnice, jsou viditelné pouhým okem.

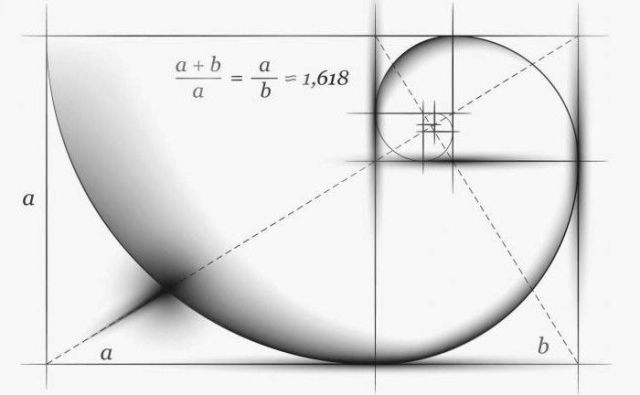
Od doby starověku zlatého poměru číslo = 1,618. Staří Řekové považovali hodnotu ideální proporce. Zlatý poměr je poměr každého následujícího čísla v řadě Fibonacci k předchozímu:

144/89=89/55=55/34=34/21=21/13=13/8=8/5=5/3=1,618...

Staří Řekové to používali v architektuře. Fasáda Parthenonu v Athénách má velmi podobné rozměry s obdélníkem postaveným na principu zlatého poměru.

Jaká je tedy krása posloupnosti vodičových úseků, jmenovitých proudů elektrických a mezních proudů jističů? Sestavte řadu čísel s následujícími hodnotami: 1,5; 2,5; 4; 6; 10; 16; 25; 40; 63...

Jmenovité proudy elektromagnetických spouštěčů:

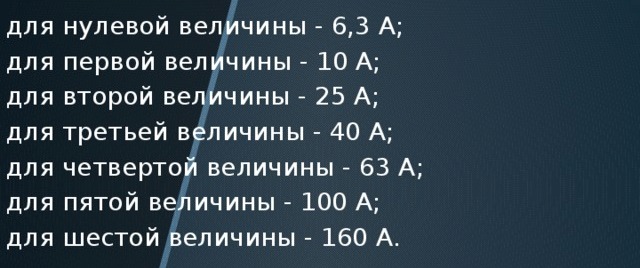
Pokud tedy rozdělíte 2,5 / 1,5; 4 / 2,5; 6,3 / 4; 10 / 6,3; 16/10; 25/16; 40/25; 63/40pak dostaneme asi 1,6. Což odpovídá zlatému pravidlu poměru. A odráží krásu a genialitu přírody i v našich nudných inženýrských systémech.

Co myslíš? Je to nehoda?

Na základě knihy „Velký román o matematice. Dějiny světa prostřednictvím hranolu matematiky“ od Michaela Loneho. Děkujeme za doporučení Vladimíra Kisela.

Alexey Bushnyaga